Lost your password? Please enter your email address. You will receive a link and will create a new password via email.
Please briefly explain why you feel this question should be reported.
Please briefly explain why you feel this answer should be reported.
Please briefly explain why you feel this user should be reported.
geometric sequence
The scenario painted in the question can be modeled as a geometric series with an initial height (term) and common ratio of $\frac{4}{5}$. We are to find the sixth term. The sum of the first 6 terms of a geometric sequence is given by $S_n=a\dfrac{1-r^n}{1-r}$, where $a$ is the first term and $r$ isRead more
The scenario painted in the question can be modeled as a geometric series with an initial height (term) and common ratio of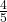
. We are to find the sixth term.
The sum of the first 6 terms of a geometric sequence is given by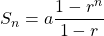
, where 
is the first term and 
is the common ratio.
Thus,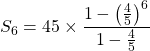
Now, we take notice that for each height, there is a rise and there is a fall. Thus, for each height, there the ball travels twice the height.
Therefore, the total distance traveled by the ball by the time it hits the ground the sixth time is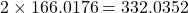
feet.
See lessApplications of Matrices
Matrices have many applications in various fields of science. One application of matrices that easily comes to mind is in computer graphics, where matrices are used for the transformation and projection of objects. Matrices are also commonly used in economics to easily represent tables and data. MatRead more
Matrices have many applications in various fields of science.
One application of matrices that easily comes to mind is in computer graphics, where matrices are used for the transformation and projection of objects.
Matrices are also commonly used in economics to easily represent tables and data.
Matrices also have various uses in optics, electrical circuits, quantum mechanics, and electronics.
It is also used in the field of geography and environmental sciences to find areas and colinearity, among other applications.
See lessQuestion of the Day (29/03/2021)
To find the derivative of the function $y=x^x$, first, we use the logarithm property to evaluate the exponent. Thus, taking the logarithm of both sides, we have $\ln y=\ln{x^x}=x\ln x$ Evaluating the derivative of both sides gives $\dfrac{1}{y}\dfrac{dy}{dx}=x\cdot\dfrac{1}{x}+\ln x$Â Â Â Â [*Note tRead more
To find the derivative of the function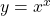
, first, we use the logarithm property to evaluate the exponent.
Thus, taking the logarithm of both sides, we have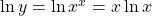
Evaluating the derivative of both sides gives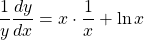
    [*Note than the right-hand side is a product so we used the product rule of differentiation.]
Solving algebraically, we have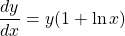
.
But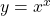
, so we have 
.
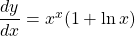Therefore, the derivative of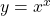
is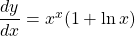 
.
See lessWhy 0 raise power 0 is equal to 1.
$0^0$ is 1 based on convention. It does not have any particular mathematical proof, however, it is a generally agreed value based on the empty-product principle. The empty product principle states that the product of "no value" is the multiplicative identity, which is 1. Hence, $0^0=1$. You can alsoRead more
The empty product principle states that the product of “no value” is the multiplicative identity, which is 1.
Hence,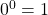
.
You can also think it that any number raised to the power of zero gives 1.
See lessDecimals and fractions
On second thought, I think the question is asking for incremental values/decremental values in hundredths starting from 8/10. Now, $\dfrac{8}{10}=0.8$, which can also be written as 0.80 to the nearest hundredth. 'Counting up' 5 hundredths gives 0.80, 0.81, 0.82, 0.83, 0.84, and 0.85. And 'counting dRead more
On second thought, I think the question is asking for incremental values/decremental values in hundredths starting from 8/10.
Now,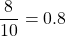
, which can also be written as 0.80 to the nearest hundredth.
‘Counting up’ 5 hundredths gives 0.80, 0.81, 0.82, 0.83, 0.84, and 0.85.
And ‘counting down’3 hundredths gives 0.80, 0.79, 0.78, and 0.77.
See lessQuestion of the Day (28/03/2021)
First, let us represent the information in a ven diagram for better understanding. Since we have three languages, we will have three intersecting circles. Let the circle labeled F, S, and C represent the people that enrolled in French, Spanish, and Chinese. Also, let $x$ represent the number of peopRead more
First, let us represent the information in a ven diagram for better understanding.
Since we have three languages, we will have three intersecting circles. Let the circle labeled F, S, and C represent the people that enrolled in French, Spanish, and Chinese. Also, let
represent the number of people that enrolled for the three languages, then:
The number of people that registered for French and Spanish only is given by
.
The number of people that registered for French and Chinese only is given by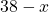
.
And the number of people that registered for Chinese and Spanish only is given by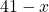
.
The information is represented in the attached Venn diagram.
Since a total of 70 people enrolled, the sum of all the parts of the Venn diagram will give us 70.
Thus,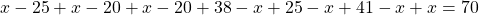
Therefore, 31 people enrolled in the three languages.
See lessWhat is taylor series?
The Tailor series of a function is an infinite sum of the terms expressed in terms of the derivatives of the function at a given point. The Tailor series of a function at a given point, $a$, is given by $f(x)=\sum_{n=0}^{\infty}\dfrac{f^{(n)}(a)}{n!}(x-a)^n$.
The Tailor series of a function is an infinite sum of the terms expressed in terms of the derivatives of the function at a given point.
The Tailor series of a function at a given point,
, is given by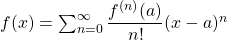 
.
See lessWhat is the intersection of 2 triangles called?
The intersection of two sides of a triangle is called a vertex. From the attached image, the point where side $a$ intersects side $b$ is called a vertex.
The intersection of two sides of a triangle is called a vertex.
From the attached image, the point where side
intersects side 
is called a vertex.
See lessEvery real number is ______ number
In the number system, a real number is a number having no imaginary part while a complex number is a number having the imaginary part. A complex number is made of the real part and the imaginary part. A complex number is represented in the rectangular form as $a+bi$, where $a$ is the real part and $Read more
In the number system, a real number is a number having no imaginary part while a complex number is a number having the imaginary part.
A complex number is made of the real part and the imaginary part. A complex number is represented in the rectangular form as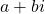
, where 
is the real part and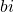 
is the imaginary part.
However, when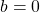
, we have 
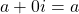, which is a real number.
Therefore, we say that every real number can be expressed as a complex number with the imaginary part equal to 0.
Therefore, “every real number is a complex number”.
See lessDecimals and fractions
Hello! I think that there is something missing from this question or the question is not worded correctly. As such I cannot understand what is actually required by your question. You may rephrase the question or provide some more information about the question so that I can understand what you mean.Read more
Hello! I think that there is something missing from this question or the question is not worded correctly. As such I cannot understand what is actually required by your question. You may rephrase the question or provide some more information about the question so that I can understand what you mean.
Note:
The hundredth is a place value system representing the second digit after the decimal point.
Examples. The value of 5 in 123.45 is 5 hundredth because 5 is the second digit after the decimal point.
The value of 2 in 0.0256 is 2 hundredth because 2 is the second digit after the decimal point.
See less