





Lost your password? Please enter your email address. You will receive a link and will create a new password via email.
Please briefly explain why you feel this question should be reported.
Please briefly explain why you feel this answer should be reported.
Please briefly explain why you feel this user should be reported.
Slope of a Function
Any slope of a function is given by the rise divided by the run. Any function where the rise is equal to the run will have a slope equal to 1. The equation of a straight line is of the form $y=mx+c$, where $m$ is the slope and $c$ is the $x$-intercept. So, any function of the form $y=x+c$, where $c$Read more
Any slope of a function is given by the rise divided by the run. Any function where the rise is equal to the run will have a slope equal to 1.
The equation of a straight line is of the form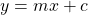 , where
, where 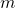 is the slope and
is the slope and  is the
is the  -intercept.
-intercept.
So, any function of the form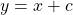 , where
, where  is any real number will have a slope of 1.
is any real number will have a slope of 1.
Examples: ,
, 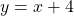 ,
, 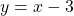 , etc.
, etc.
See lessWhat is Zero Factorial equal to
Zero factorial (0!) is equal to 1 by the empty-product convention. The empty-product convention is the result of multiplying no factors and is equal to the multiplicative identity which is 1.
Zero factorial (0!) is equal to 1 by the empty-product convention.
The empty-product convention is the result of multiplying no factors and is equal to the multiplicative identity which is 1.
See lessWhat is integral function
An integral function is a function defined by integration. The integral of a function $y=f(x)$ is the area under the curve of $f(x)$. That is the area of the portion bounded by the curve, $f(x)$, and the $x$-axis.
An integral function is a function defined by integration.
The integral of a function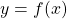 is the area under the curve of
is the area under the curve of 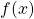 .
.
That is the area of the portion bounded by the curve,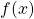 , and the
, and the  -axis.
-axis.
See lesswhat is crammer rule?
Cramer's rule is a method of solving a system of linear equations using determinants of matrices.
Cramer’s rule is a method of solving a system of linear equations using determinants of matrices.
See lessFourier Analysis
The given periodic function can be rewritten as $f(t)=\begin{cases} 1 & \text{ if } 0<t<0.2 \\ 3 & \text{ if } 0.2<t<0.4 \end{cases}$ $f(t+0.4)=f(t)$ The Fourier series expansion of a function $f(t)$ with period, $T$, is given by $f(t)=\dfrac{a_0}{2}+\sum_{n=1}^{\infty}{\left\{a_Read more
The given periodic function can be rewritten as
The Fourier series expansion of a function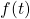 with period,
with period, 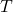 , is given by
, is given by 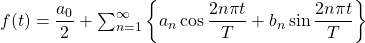 , where
, where 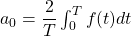 ,
, 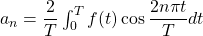 , and
, and 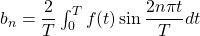
Here,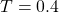 , so we have:
, so we have: 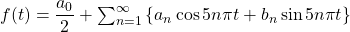 .
.
Where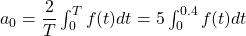
=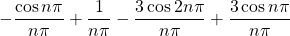
=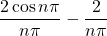
Therefore, the Fourier series is given by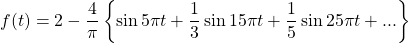 .
.
See lessQuestion of the Day (27/03/2021)
a.) The mean/average of a set of data is given by the total score divided by the count of the data. Thus, $\text{Mean}=\dfrac{22+22+19+31+36+50+38+25+30}{9}=\dfrac{273}{9}=30.33$. b.) The median is the score at the center when the set of data is arranged in order. Thus, arranging the set of dRead more
a.) The mean/average of a set of data is given by the total score divided by the count of the data.
Thus,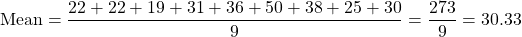 .
.
b.) The median is the score at the center when the set of data is arranged in order.
Thus, arranging the set of data, we have: 19, 22, 22, 25, 30, 31, 36, 38, 50.
Therefore, the median is 30.
c.) The mode is the most occurring score. 22 occurred twice whereas other numbers occurred once.
Therefore, the mode is 22.
See lessQuestion of the Day (26/03/2021)
A zero of a function is a value of the function when the function equals zero. For example, given the function $f(x)$, the zeros of $f(x)$ are the values of $x$ when $f(x)=0$. 2. (a) For the function $y=3x^2+2x-5$, the zeros of the function are the value of $x$, when $3x^2+2x-5=0$. Solving $3x^2+2x-Read more
2.
(a) For the function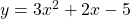 , the zeros of the function are the value of
, the zeros of the function are the value of  , when
, when 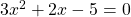 .
.
Solving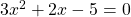 by grouping and factorizing gives
by grouping and factorizing gives 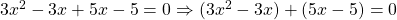
Therefore, the zeros of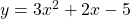 are
are 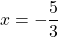 and
and 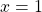
(b) For the function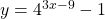 , the zeros of the function are the value of
, the zeros of the function are the value of  , when
, when  or
or 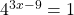 .
.
Recall that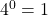 .
.
So, we have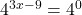
Equating the exponents, we have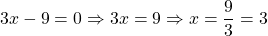 .
.
Therefore, the zero of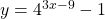 is at
is at 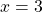 .
.
(c) For the function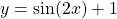 ;
; 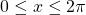 , the zeros of the function are the value of
, the zeros of the function are the value of  between 0 and
between 0 and 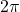 , where
, where 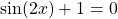 or
or 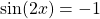 .
.
For n = 0,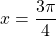
For n =1,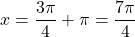
For n =2,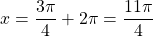 which is greater than
which is greater than 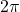 .
.
Therefore, the zeros of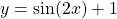 ;
; 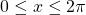 are
are 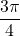 and
and 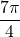 .
.
See lessMethods of Factorization
There are many methods of factorisation. The three commonest types are: 1) Factorisation by factoring out the GCD. Example: Factor $3x^2+6x$. Here, the GCD (the greatest factor both terms have in common) is $3x$. So, factoring out $3x$ gives $3x(x+2)$. Therefore, $3x^2+6x=3x(x+2)$. 2) FactoriRead more
There are many methods of factorisation.
The three commonest types are:
1) Factorisation by factoring out the GCD.
Example: Factor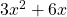 .
.
Here, the GCD (the greatest factor both terms have in common) is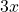 . So, factoring out
. So, factoring out 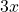 gives
gives 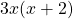 .
.
Therefore,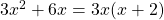 .
.
2) Factorisation by grouping.
Example: to factor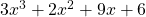 , we group it as follows:
, we group it as follows: 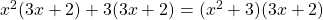 .
.
Therefore,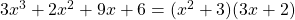 .
.
3.) Factoring quadratic trinomials by trial and error.
Example: To factor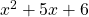 , we use the formula
, we use the formula 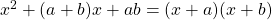 . So, here, we have
. So, here, we have 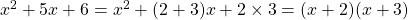 .
.
Therefore,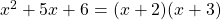 .
.
See lessQuestion of the Day (23/03/2021)
The future value (FV) of an investment (P) at an annual compound interest rate of (r) compounded $t$ times a year for $n$ years is given by $FV=P\left(1+\dfrac{r}{t}\right)^{nt}$ Here: $P=$\$$8,000, r=8\%=0.08, n=9\text{ months}=\dfrac{9}{12}\text{ years}$. Since the CD is compounded monthly, that mRead more
The future value (FV) of an investment (P) at an annual compound interest rate of (r) compounded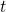 times a year for
times a year for 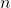 years is given by
years is given by
Here: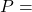 $
$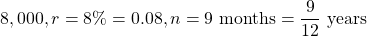 .
.
Since the CD is compounded monthly, that means that in a year it will be compounded 12 times, so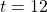 .
.
Substituting all values into the formula, we have:
Therefore, the value of her investment at the maturity of the CD is $8,493.00.
See lessEquivalent Fractions
Equivalent fractions are fractions which when simplified to the lowest term give the same fraction. Equivalent fractions are obtained by multiplying/dividing the numerator and the denominator of a fraction by a common factor. Given the fraction $\dfrac{4}{5}$, multiplying the numerator and the denomRead more
Equivalent fractions are fractions which when simplified to the lowest term give the same fraction. Equivalent fractions are obtained by multiplying/dividing the numerator and the denominator of a fraction by a common factor.
Given the fraction , multiplying the numerator and the denominator by 2 gives
, multiplying the numerator and the denominator by 2 gives 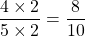 .
.
Multiplying the numerator and the denominator by 3 gives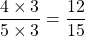 .
.
Multiplying the numerator and the denominator by 4 gives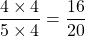 .
.
Thus,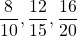 are equivalent fractions to
are equivalent fractions to  .
.
See less