





Lost your password? Please enter your email address. You will receive a link and will create a new password via email.
Please briefly explain why you feel this question should be reported.
Please briefly explain why you feel this answer should be reported.
Please briefly explain why you feel this user should be reported.
Probability and Statistics
First, let us confirm that all the class' scores were covered by making sure that the sum of all probabilities is 1. Thus, $\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{6}=\dfrac{3}{6}+\dfrac{2}{6}+\dfrac{1}{6}=\dfrac{6}{6}=1$. Thus, the scores of the entire class are represented. The LCD of the denominatorsRead more
First, let us confirm that all the class’ scores were covered by making sure that the sum of all probabilities is 1.
Thus,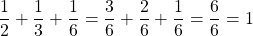 .
.
Thus, the scores of the entire class are represented.
The LCD of the denominators is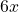 , so let the total number of students in the class be
, so let the total number of students in the class be 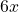 , then
, then 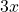 students scored 90,
students scored 90, 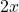 students scored 87, and
students scored 87, and  students scored 89.
students scored 89.
Thus, the average grade of the entire class is given by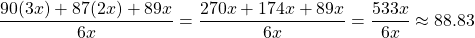 .
.
See lessApplied Mathematics: Kinematics
The relationship between the vertical height, h, the time, t, the initial velocity, u, and the acceleration due to gravity, g, is given by $h=ut+\dfrac{1}{2}gt^2$. Here, $h=56$ m, $u=0$, $g=9.8 m/s^2$. Thus, $56=0\times t+\dfrac{1}{2}9.8t^2\Rightarrow56=4.9t^2\Rightarrow t^2=\dfrac{56}{4.9}=11.42857Read more
The relationship between the vertical height, h, the time, t, the initial velocity, u, and the acceleration due to gravity, g, is given by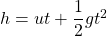 .
.
Here,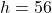 m,
m, 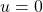 ,
, 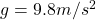 .
.
Thus,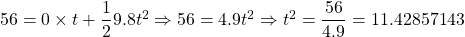
Using,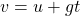 , we have
, we have 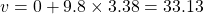 m/s.
m/s.
See lessalgebra questions
Using a graphing calculator, we can approximate $k$ to be 5.2 or 0.8. (as attached).
Using a graphing calculator, we can approximate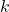 to be 5.2 or 0.8. (as attached).
to be 5.2 or 0.8. (as attached).
See lessGeometry Practice: Circle
Let the length of the sides of the original square be $s$, then the diameter of the circle cut-off from the square is $s$. Now, the diagonal of the square cut-off from the circle is equivalent to the diameter of the circle, thus $s$. Now, the area of a square given the length of the diagonal is giveRead more
Let the length of the sides of the original square be , then the diameter of the circle cut-off from the square is
, then the diameter of the circle cut-off from the square is  .
.
Now, the diagonal of the square cut-off from the circle is equivalent to the diameter of the circle, thus .
.
Now, the area of a square given the length of the diagonal is given by half the square of the length of the diagonal.
Therefore, the area of the square cut-off is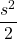 . That is half the square of the length of the sides of the original square.
. That is half the square of the length of the sides of the original square.
See lessHow can you identify if the sequence is arithmetic or geometric
A sequence is an arithmetic sequence if each term is obtained by the addition or subtraction of a constant from the preceding term. A sequence is a geometric sequence if each term is obtained by the multiplication or division of a constant from the preceding term.
A sequence is an arithmetic sequence if each term is obtained by the addition or subtraction of a constant from the preceding term.
A sequence is a geometric sequence if each term is obtained by the multiplication or division of a constant from the preceding term.
See lessGeometry of Motion (kinematics)……………..
Note that 1 knot = 1 nautical mile per hour (1 nm/hr). The time spent by the boat to travel from port A to port B is given by $\dfrac{9\text{ nautical mile}}{18\text{ nautical mile per hour}}=0.5\text{ hours}$. The time spent by the boat to travel from port B back to port A is $\dfrac{9\text{ nauticRead more
Note that 1 knot = 1 nautical mile per hour (1 nm/hr).
The time spent by the boat to travel from port A to port B is given by .
.
The time spent by the boat to travel from port B back to port A is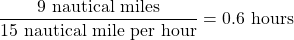 .
.
Thus, the total distance traveled is 9 nm + 9 nm = 18 nm, and the total time taken is 0.5 hours + 0.6 hours = 1.1 hours.
Therefore, the average speed is the total distance traveled divided by the total time taken =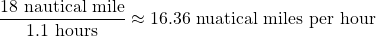 .
.
See lessAlgebraic Expression
An algebraic expression is a mathematics statement where variables and constants are combined using the arithmetic operations of addition, subtraction, multiplication, and division.
An algebraic expression is a mathematics statement where variables and constants are combined using the arithmetic operations of addition, subtraction, multiplication, and division.
See lessCircle Problem in mathematics
The area, $A$, of a circle of radius, $r$, is given by $A=\pi r^2$. When the radius is decreased by 10%, the new radius is $\dfrac{100\%-10\%}{100\%}r=\dfrac{90\%}{100\%}r=0.9r$. Then, the new area is $A=\pi (0.9r)^2=0.81\pi r^2=0.81\times\text{ area of the original circle}$. Therefore, the new areaRead more
The area,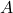 , of a circle of radius,
, of a circle of radius,  , is given by
, is given by 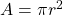 .
.
When the radius is decreased by 10%, the new radius is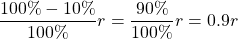 .
.
Then, the new area is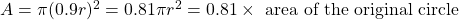 .
.
Therefore, the new area is an 100% – 81% = 19% decrease from the original area.
See lessMathematics Problem (Permutation)
Any of the 8 swimmers can take the 1st prize. After the first price, there are 7 swimmers left, and any of the 7 swimmers can take the second prize. Similarly, after the second price, there are 6 swimmers left, and any of the 6 swimmers can take the third prize. Therefore, the number of possible outRead more
Any of the 8 swimmers can take the 1st prize.
After the first price, there are 7 swimmers left, and any of the 7 swimmers can take the second prize.
Similarly, after the second price, there are 6 swimmers left, and any of the 6 swimmers can take the third prize.
Therefore, the number of possible outcomes is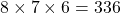 .
.
See lessMathematics (Data)
The first quartile (Q1) of a set of data is the data point that divides the set of data into the first 25% versus the last 75% after the dataset has been arranged in order (usually ascending order). This is the data point dividing the first half of a dataset into two equal parts after the dataset isRead more
The first quartile (Q1) of a set of data is the data point that divides the set of data into the first 25% versus the last 75% after the dataset has been arranged in order (usually ascending order). This is the data point dividing the first half of a dataset into two equal parts after the dataset is arranged.
Thus, arranging the given data in ascending order, we have 56, 59, 59, 62, 63, 64, 66, 67, 73, 77, 78, 78, 83, 84, 85, 86, 90, 97
There are 18 data points in the dataset, thus there are 9 data points in each half. The first half of the dataset is 56, 59, 59, 62, 63, 64, 66, 67, 73. The halfway (median) is obtained by counting out 4 data points from both ends, which leaves 63 at the center, thus the middle number of the first set is 63 and hence Q1 is 63.
See less