Lost your password? Please enter your email address. You will receive a link and will create a new password via email.
Please briefly explain why you feel this question should be reported.
Please briefly explain why you feel this answer should be reported.
Please briefly explain why you feel this user should be reported.
Theorems on Trapezoid
A trapezoid is a quadrilateral (shape of 4 sides), and hence the sum of the interior angles of a quadrilateral is $360^o$. Thus, $63^o+90^o+90^o+n^o=360^o\Rightarrow243^o+n^o=360^o\Rightarrow n^o=360^o-243^o=117^o$. Therefore, $n=117$.
A trapezoid is a quadrilateral (shape of 4 sides), and hence the sum of the interior angles of a quadrilateral is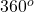
.
Thus,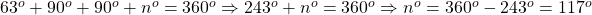
.
Therefore,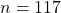
.
See lessMean of frequency table
The mean of a set of numbers, $x_i$, is given by the sum of the numbers divided by the count of the numbers, $n$. That is, mean ($\bar{x}$) $=\dfrac{\sum{x_i}}{n}$. Given a set of numbers with the frequencies, the the mean is given by $\bar{x}=\dfrac{\sum{fx_i}}{\sum{f}}$.
The mean of a set of numbers,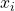
, is given by the sum of the numbers divided by the count of the numbers, 
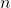. That is, mean (
) 
.
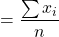Given a set of numbers with the frequencies, the the mean is given by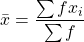
.
See lessEquilateral Triangle
An equilateral triangle is a triangle that has the three sides congruent and the measures of the three internal angles equal. The sum of the interior angles of a triangle is $180^o$. Since all the angles of an equilateral triangle are equal, then each angle of an equilateral triangle measures $\dfraRead more
An equilateral triangle is a triangle that has the three sides congruent and the measures of the three internal angles equal.
The sum of the interior angles of a triangle is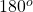
. Since all the angles of an equilateral triangle are equal, then each angle of an equilateral triangle measures 
.
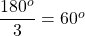Therefore, the measure of each angle of an equilateral triangle is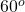
.
See lessThe uses of the first and second derivative to determine the intervals of increase and decrease of a function.
Given a function, , by the first derivative test, the function is increasing in the intervals where and decreasing in the intervals where .
Given a function,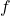
, by the first derivative test, the function is increasing in the intervals where 
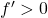and decreasing in the intervals where 
.
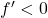See lessThe uses of the first and second derivative to determine the intervals of increase and decrease of a function.
Given a function, $f$, by the first derivative test, the function is increasing in the intervals where $f'>0$ and decreasing in the intervals where $f'<0$. Thus, given $f(x)=(x+3)(x–2)^3$, $f'(x)=(x+3)\cdot3(x-2)^2+(x-2)^3=3(x+3)(x-2)^2+(x-2)^3$ $=(x-2)^2(3x+9+x-2)=(x-2)^2(4x+7)$. The turningRead more
Given a function,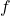
, by the first derivative test, the function is increasing in the intervals where 
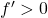and decreasing in the intervals where 
.
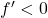Thus, given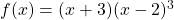
, 
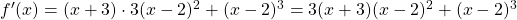
The turning poions are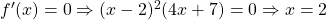
or 
.
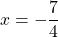Thus, the turning points divives the domain into three regions, namely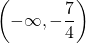
, 
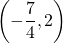, and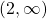 
.
Testing points on the interval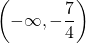
, 
.
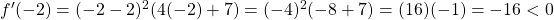Thus, the function is decreasing on the interval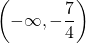
Testing points on the interval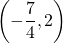
, 
.
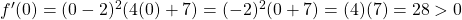Thus, the function is increasing on the interval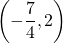
.
Testing points on the interval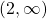
, 
.
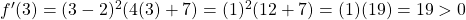Thus, the function is increasing on the interval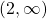
.
See lesswhat is x² + 8x + 20
Your question is not clear enough. If you are asking what type of expression $x^2-8x-20$ is, then because the highest power of the variable is 2, $x^2-8x-20$ is a quadratic equation. An algebraic expression with 2 as the highest power of the variable is called a quadratic equation.
Your question is not clear enough.
If you are asking what type of expression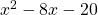
is, then because the highest power of the variable is 2, 
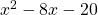is a quadratic equation.
An algebraic expression with 2 as the highest power of the variable is called a quadratic equation.
See lesswhat type of algebraic equation is 2x+5?
An algebraic expression that has 1 as the highest power of the exponent is called a linear expression. $2x+5$ has 1 as the highest power of the variable, $x$, thus it is a linear equation.
An algebraic expression that has 1 as the highest power of the exponent is called a linear expression.
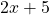has 1 as the highest power of the variable, 
, thus it is a linear equation.
See lessMathematical question
An algebraic term that contains three terms is called a trinomial.
An algebraic term that contains three terms is called a trinomial.
See lesswhat is metric space?
A metric space is a set together with a function (called the metric) that defines the distance between any two members (points) of the set.
A metric space is a set together with a function (called the metric) that defines the distance between any two members (points) of the set.
See lessProbability of drawing in a deck of cards
When two cards are picked from a deck of cards, there are two cases, namely, with replacement and without replacement. Case 1: With replacement There are 4 aces, 4 kings, and a total of 52 cards in a standard deck of card. The probability of picking an ace is $\dfrac{4}{52}=\dfrac{1}{13}$ and the prRead more
When two cards are picked from a deck of cards, there are two cases, namely, with replacement and without replacement.
Case 1: With replacement
There are 4 aces, 4 kings, and a total of 52 cards in a standard deck of card.
The probability of picking an ace is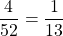
and the probability of picking a king is 
.
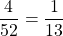Thus, the probability of picking an ace AND a king is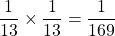
.
Case 1: Without replacement
There are 4 aces, 4 kings, and a total of 52 cards for the first pick and a total of 51 cards for the second pick in a standard deck of card.
The probability of picking an ace first is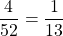
and the probability of picking a king next is 
.
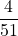Thus, the probability of picking an ace AND a king is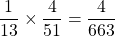
.
See less