Lost your password? Please enter your email address. You will receive a link and will create a new password via email.
Please briefly explain why you feel this question should be reported.
Please briefly explain why you feel this answer should be reported.
Please briefly explain why you feel this user should be reported.
what is the slope-intercept of this linear equation?
The slope-intercept form of the equation of a straight line is given by $y=mx+c$, where $m$ is the slope of the line and $c$ is the $y$-intercept. Given the line $2x-4y-12=0$ Adding 12 and subtracting 2x to both sides, we have $2x-4y-12+12-2x=0+12-2x\Rightarrow-4y=-2x+12$. Dividing through by -4 givRead more
The slope-intercept form of the equation of a straight line is given by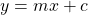
, where 
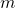is the slope of the line and 
is the 
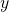-intercept.
Given the line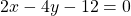
Adding 12 and subtracting 2x to both sides, we have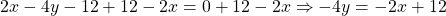
.
Dividing through by -4 gives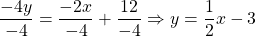
.
Therefore, the slope-intercept form of the equation of the line is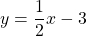
.
See lessProblem Solving
Let the length and the width of the rectangle be $l$ and $w$ respectively, then the area of the rectangle is given by $lw=300$ . . . . . (1) and the perimeter is given by $2(l+w)=70\Rightarrow l+w=\dfrac{70}{2}=35$ . . . . . (2). From the second equation, $l=35-w$ . . . . . (3). Substituting the thiRead more
Let the length and the width of the rectangle be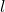
and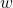 
respectively, then the area of the rectangle is given by 
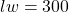. . . . . (1) and the perimeter is given by 
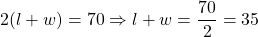. . . . . (2).
From the second equation,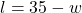
. . . . . (3).
Substituting the third equation into the first equation, we have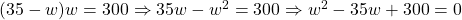
.
Thus,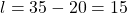
or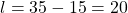 
.
Therefore, taking that the length is greater than the width, then the length of the rectangle is 20 meters and the width is 15 meters.
See lesswhat is a³×a⁴ =
Using the law of exponents, $a^x\times a^y=a^{x+y}$. Therefore, $a^3\times a^4=a^{3+4}=a^7$.
Using the law of exponents,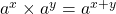
.
Therefore,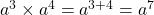
.
See lessTrigonometry problem:
Let the distance between John's positing and the electric post be $d$, then using the right-triangle trigonometric identities, we have $\tan\theta=\dfrac{\text{opposite}}{\text{adjacent}}$. Thus, $\tan42.5^o=\dfrac{10}{d}$. Taking the reciprocal of both sides, we have $\dfrac{1}{\tan42.5^o}=\dfrac{dRead more
Let the distance between John’s positing and the electric post be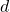
, then using the right-triangle trigonometric identities, we have 
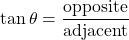. Thus, 
.
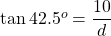Taking the reciprocal of both sides, we have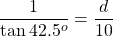
, and multiplying both sides by 10, we have 
.
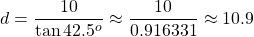Therefore, John is standing about 10.9 meters from the electric post.
See lessTrigonometry Problem
Let the angle of elevation be $\theta$, then using the right-triangle trigonometric identities, $\tan\theta=\dfrac{\text{opposite}}{\text{adjacent}}=\dfrac{25}{10}=2.5$. Thus, $\theta=\tan^{-1}2.5\approx68.2^o$. Therefore, the angle of elevation is $68.2^o$.
Let the angle of elevation be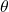
, then using the right-triangle trigonometric identities, 
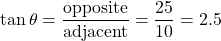. Thus, 
.
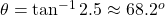Therefore, the angle of elevation is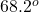
.
See lessTrigonometry problem
Using the right-triangle trigonometry identities, we have $\tan18^o=\dfrac{h}{100}$. Multiplying both sides by 100, we have $h=100\tan18^o=100\times0.324920\approx32.5$. Therefore, the height of the tree is about 32.5 meters.
Using the right-triangle trigonometry identities, we have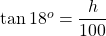
.
Multiplying both sides by 100, we have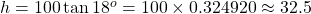
.
Therefore, the height of the tree is about 32.5 meters.
See lessStatistics and Probability
Probability is a chance of an event happening. The probability of an event, P(E), is given by $P(E)=\dfrac{\text{number of events, E}}{\text{Total possible outcomes}}$. Thus, in the class, there are 3 girls and a total of 3 + 5 = 8 students. Therefore, the probability that the volunteer is a girl isRead more
Probability is a chance of an event happening. The probability of an event, P(E), is given by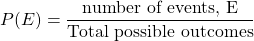
.
Thus, in the class, there are 3 girls and a total of 3 + 5 = 8 students.
Therefore, the probability that the volunteer is a girl is
P(girl)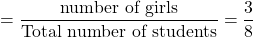
.
See lessProblem solving
Ratio is a comparison between two or more quantities indicating the amount of one quantity in the others. To find the value between quantity A with a value $a$ and quantity B with a value $b$, we write Quantity A : Quantity B = $a:b$. [the colon (:) is read "it to"] Thus, given that there areRead more
Ratio is a comparison between two or more quantities indicating the amount of one quantity in the others. To find the value between quantity A with a value
and quantity B with a value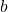 
, we write Quantity A : Quantity B = 
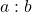. [the colon (:) is read “it to”]
Thus, given that there are 860 female followers out of a total of 1260 followers, this means that there are 1260 – 860 = 400 male followers.
Therefore, the ratio of female to male followers is number of female followers : number of male followers = 860 : 400 = 43 : 20 [divide through by the GCD].
Answer: 43 : 20
See lessProblem solving
The area (A) of a triangle is given by , where is the length of the base and is the height. Here square inches and inches. Thus, Multiplying both sides by 2 gives or or But b is a length and has to be positive so . Therefore, the base is 14 inches and the height is 14 – 7 = 7 inches.
The area (A) of a triangle is given by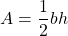
, where 
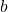is the length of the base and 
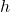is the height.
Here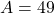
square inches and 
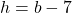inches.
Thus,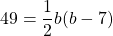
Multiplying both sides by 2 gives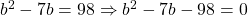
But b is a length and has to be positive so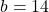
.
Therefore, the base is 14 inches and the height is 14 – 7 = 7 inches.
See lessProblem solving
The area (A) of a triangle is given by $A=\dfrac{1}{2}bh$, where $b$ is the length of the base and $h$ is the height. Here $A=49$ square inches and $h=b-7$ inches. Thus, $49=\dfrac{1}{2}b(b-7)$ Multiplying both sides by 2 gives $b^2-7b=98\Rightarrow b^2-7b-98=0$ $\Rightarrow(b-14)(b+7)=0$ $\RightarrRead more
The area (A) of a triangle is given by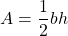
, where 
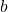is the length of the base and 
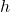is the height.
Here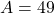
square inches and 
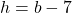inches.
Thus,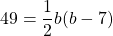
Multiplying both sides by 2 gives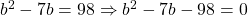
But b is a length and has to be positive so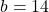
.
Therefore, the base is 14 inches and the height is 14 – 7 = 7 inches.
See less