





Lost your password? Please enter your email address. You will receive a link and will create a new password via email.
Please briefly explain why you feel this question should be reported.
Please briefly explain why you feel this answer should be reported.
Please briefly explain why you feel this user should be reported.
In mathematics, a __________ is used to display the overlap and distinctions among sets.
A Venn diagram is a visual tool used to represent the relationship between sets. It consists of one or more circles that overlap or intersect, with each circle representing a specific set. The overlapping regions show where sets have elements in common, while the non-overlapping parts display elemenRead more
A Venn diagram is a visual tool used to represent the relationship between sets. It consists of one or more circles that overlap or intersect, with each circle representing a specific set. The overlapping regions show where sets have elements in common, while the non-overlapping parts display elements unique to each set. The circles are enclosed inside a rectangle which represents the universal set.
For example, consider the universal set containing positive integers less than 10, and consider two sets: Set A, which contains even numbers, and Set B, which contains multiples of 3.
A Venn diagram for these sets would have one circle representing even numbers and another circle representing multiples of 3. The overlapping section would represent numbers that are both even and multiples of 3, which in this case is 6. The other numbers that are neither even numbers nor multiples of 3 are placed within the rectangle but outside the circles.

See lessDifferentiate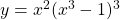 wrt x
wrt x
To differentiate the function $y = x^2(x^3 - 1)^3$ with respect to $x$, we can use the product rule. The product rule states that if you have a function of the form $u(x)v(x)$, the derivative is given by: $$\dfrac{d}{dx}[u(x)v(x)] = u(x)v'(x) + u'(x)v(x)$$ In this case, let $u(x) = x^2$ and $v(x) =Read more
To differentiate the function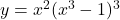 with respect to
with respect to  , we can use the product rule. The product rule states that if you have a function of the form
, we can use the product rule. The product rule states that if you have a function of the form 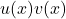 , the derivative is given by:
, the derivative is given by:
In this case, let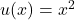 and
and 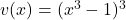 . We need to find their derivatives:
. We need to find their derivatives:
1.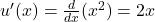 (using the power rule).
(using the power rule).
2. We can find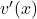 using the chain rule. The chain rule states that if you have a composite function, such as
using the chain rule. The chain rule states that if you have a composite function, such as 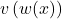 , the derivative of
, the derivative of 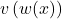 with respect to
with respect to  is given by:
is given by:
To find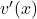 , let
, let 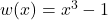 , so
, so 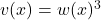 :
:
Now, we need to find![Rendered by QuickLaTeX.com \frac{d}{dx}[w(x)]](https://acedstudy.com/wp-content/ql-cache/quicklatex.com-36d421773cfe565ffe6e0c08aa5fa6a3_l3.png) :
:
Now, we can compute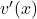 :
:
Now, apply the product rule to find![Rendered by QuickLaTeX.com \frac{d}{dx}[x^2(x^3 - 1)^3]](https://acedstudy.com/wp-content/ql-cache/quicklatex.com-971bf968bb9ec6dc561cd28051c15705_l3.png) :
:
Now, simplify this expression:
So, the derivative of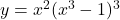 with respect to
with respect to  is:
is:
![Rendered by QuickLaTeX.com \[\frac{d}{dx}[x^2(x^3 - 1)^3] &= 9x^4(x^3 - 1)^2 + 2x(x^3 - 1)^3\]](https://acedstudy.com/wp-content/ql-cache/quicklatex.com-667be81b95afd08eaf12d75a3b58dada_l3.png)
See lessDifferentiate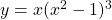 wrt x
wrt x
To differentiate the function $y = x(x^2 - 1)^3$ with respect to $x$, you can apply both the product rule and the chain rule. Using the product rule, which states that $\dfrac{d}{dx}\left[u(x)v(x)\right] = u(x)v'(x) + u'(x)v(x)$, we have: Let $u(x) = x$ and $v(x) = (x^2 - 1)^3$. We know that $u'(x)Read more
To differentiate the function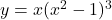 with respect to
with respect to  , you can apply both the product rule and the chain rule.
, you can apply both the product rule and the chain rule.
Using the product rule, which states that![Rendered by QuickLaTeX.com \dfrac{d}{dx}\left[u(x)v(x)\right] = u(x)v'(x) + u'(x)v(x)](https://acedstudy.com/wp-content/ql-cache/quicklatex.com-7a2a5485655cf03025fd08c6600e8169_l3.png) , we have:
, we have:
Let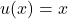 and
and 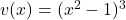 .
.
We know that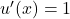 (the derivative of
(the derivative of  is 1).
is 1).
Now, we need to find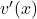 , which involves applying the chain rule because
, which involves applying the chain rule because 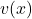 is a composite function. The chain rule states that if you have a composite function, such as
is a composite function. The chain rule states that if you have a composite function, such as 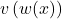 , the derivative of
, the derivative of 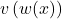 with respect to
with respect to  is given by:
is given by:
Let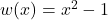 , so
, so 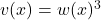 .
.
Now, we can find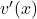 :
:
Now, we find![Rendered by QuickLaTeX.com \dfrac{d}{dx}[w(x)]](https://acedstudy.com/wp-content/ql-cache/quicklatex.com-821c4998113fb8892e2cd59f24c6c677_l3.png) :
:
Now, we can compute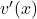 :
:
Now, apply the product rule:
Now, simplify this expression:
So, the correct derivative of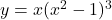 with respect to
with respect to  is:
is:
![Rendered by QuickLaTeX.com \[\dfrac{d}{dx}[x(x^2 - 1)^3] &= 6x^2(x^2 - 1)^2 + (x^2 - 1)^3\]](https://acedstudy.com/wp-content/ql-cache/quicklatex.com-5f9e918c9e4bc6e1db5271a1203d6465_l3.png)
See lessDifferentiate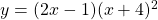 wrt x
wrt x
To differentiate the function $y = (2x - 1)(x + 4)^2$ with respect to $x$, you can use the product rule. The product rule states that if you have a function of the form $u(x)v(x)$, the derivative is given by: $\dfrac{d}{dx}\left[u(x)v(x)\right] = u(x)v'(x) + u'(x)v(x)$. In this case, let $u(x) = 2xRead more
To differentiate the function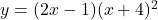 with respect to
with respect to  , you can use the product rule. The product rule states that if you have a function of the form
, you can use the product rule. The product rule states that if you have a function of the form 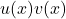 , the derivative is given by:
, the derivative is given by:
In this case, let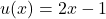 and
and 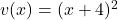 .
.
Now, we’ll find their derivatives:
To find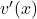 , you can use the chain rule. The chain rule states that if you have a composite function, such as
, you can use the chain rule. The chain rule states that if you have a composite function, such as 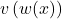 , the derivative of
, the derivative of 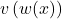 with respect to
with respect to  is given by:
is given by:
Let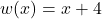 , so
, so 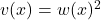 . Now, we can find
. Now, we can find 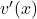 :
:
So,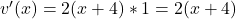 .
.
Now, apply the product rule:
Now, simplify this expression:
You can further simplify this expression if needed, but this is the derivative of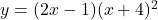 with respect to
with respect to  :
:
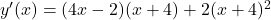 .
.
See lessDifferentiate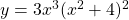 wrt x
wrt x
To differentiate the function $y = 3x^3(x^2 + 4)^2$ with respect to $x$, you can use the product rule. The product rule states that if you have a function of the form $u(x)v(x)$, the derivative is given by: $\dfrac{d}{dx}\left[u(x)v(x)\right] = u(x)v'(x) + u'(x)v(x)$. In this case, let $u(x) = 3x^3$Read more
To differentiate the function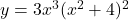 with respect to
with respect to  , you can use the product rule. The product rule states that if you have a function of the form
, you can use the product rule. The product rule states that if you have a function of the form 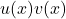 , the derivative is given by:
, the derivative is given by:
In this case, let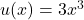 and
and 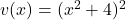 .
.
Now, we’ll find their derivatives:
To find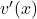 , you can use the chain rule. The chain rule states that if you have a composite function, such as
, you can use the chain rule. The chain rule states that if you have a composite function, such as 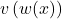 , the derivative of
, the derivative of 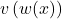 with respect to
with respect to  is given by:
is given by:
Let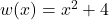 , so
, so 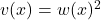 .
.
Now, we can find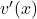 :
:
So,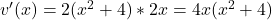 .
.
Now, apply the product rule:
Now, simplify this expression:
So, the derivative of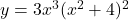 with respect to
with respect to  is:
is:
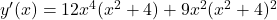 .
.
See lessDifferentiate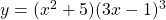 wrt x
wrt x
To differentiate the function $y = (x^2 + 5)(3x - 1)^3$ with respect to $x$, you can use the product rule. The product rule states that if you have a function of the form $u(x)v(x)$, the derivative is given by: $\dfrac{d}{dx}\left[u(x)v(x)\right] = u(x)v'(x) + u'(x)v(x)$. In this case, let $u(x) = xRead more
To differentiate the function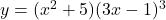 with respect to
with respect to  , you can use the product rule. The product rule states that if you have a function of the form
, you can use the product rule. The product rule states that if you have a function of the form 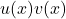 , the derivative is given by:
, the derivative is given by:
In this case, let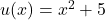 and
and 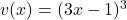 .
.
Now, we’ll find their derivatives:
To find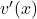 , we’ll need to use the chain rule. The chain rule states that if you have a composite function, such as
, we’ll need to use the chain rule. The chain rule states that if you have a composite function, such as 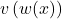 , the derivative of
, the derivative of 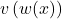 with respect to
with respect to  is given by:
is given by:
Let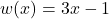 , so
, so 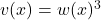 .
.
Now, we can find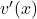 :
:
So,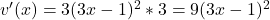 .
.
Now, apply the product rule:
Now, simplify this expression:
So, the derivative of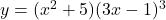 with respect to
with respect to  is:
is:
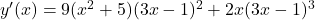 .
.
See lessDifferentiate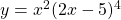 wrt x
wrt x
To differentiate the function $y = x^2(2x - 5)^4$ with respect to $x$, you use the product rule. The product rule states that if you have a function of the form $u(x)v(x)$, the derivative is given by: $\dfrac{d}{dx}\left[u(x)v(x)\right] = u(x)v'(x) + u'(x)v(x)$. In this case, let $u(x) = x^2$ and $vRead more
To differentiate the function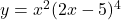 with respect to
with respect to  , you use the product rule.
, you use the product rule.
The product rule states that if you have a function of the form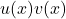 , the derivative is given by:
, the derivative is given by:
In this case, let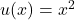 and
and 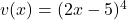 .
.
Now, we’ll find their derivatives:
To find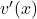 , we’ll need to use the chain rule. The chain rule states that if you have a composite function, such as
, we’ll need to use the chain rule. The chain rule states that if you have a composite function, such as 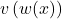 , the derivative of
, the derivative of 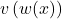 with respect to
with respect to  is given by:
is given by:
Let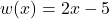 , so
, so 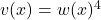 . Now, we can find
. Now, we can find 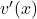 :
:
So,
Now, we can apply the product rule:
Now, simplify this expression:
So, the corrected derivative of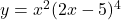 with respect to
with respect to  is:
is:
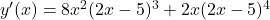 .
.
See lessDifferentiate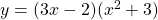 wrt x
wrt x
To differentiate the function $y = (3x - 2)(x^2 + 3)$ with respect to $x$, you can use the product rule, which states that the derivative of a product of two functions is given by: $\frac{d}{dx}\left[u(x)v(x)\right] = u(x)v'(x) + u'(x)v(x)$, where $u(x)$ and $v(x)$ are functions of $x$, and $u'(x)$Read more
To differentiate the function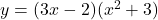 with respect to
with respect to  , you can use the product rule, which states that the derivative of a product of two functions is given by:
, you can use the product rule, which states that the derivative of a product of two functions is given by:
where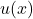 and
and 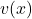 are functions of
are functions of  , and
, and 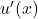 and
and 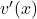 are their respective derivatives with respect to
are their respective derivatives with respect to  .
.
In this case, let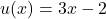 and
and 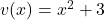 .
.
Now, let’s find their derivatives:
Now, apply the product rule:
Now, simplify this expression:
Combine like terms:
So, the derivative of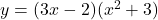 with respect to
with respect to  is:
is:
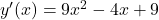 .
.
See lessA __________ illustrates how sets intersect and differ from one another.
A Venn diagram is a visual tool used to represent the relationship between sets. It consists of one or more circles that overlap or intersect, with each circle representing a specific set. The overlapping regions show where sets have elements in common, while the non-overlapping parts display elemenRead more
A Venn diagram is a visual tool used to represent the relationship between sets. It consists of one or more circles that overlap or intersect, with each circle representing a specific set. The overlapping regions show where sets have elements in common, while the non-overlapping parts display elements unique to each set. The circles are enclosed inside a rectangle which represents the universal set.
For example, consider the universal set containing positive integers less than 10, and consider two sets: Set A, which contains even numbers, and Set B, which contains multiples of 3.
A Venn diagram for these sets would have one circle representing even numbers and another circle representing multiples of 3. The overlapping section would represent numbers that are both even and multiples of 3, which in this case is 6. The other numbers that are neither even numbers nor multiples of 3 are placed within the rectangle but outside the circles.
A __________(Venn diagram, line plot) shows the relationship between sets.
A Venn diagram is a visual tool used to represent the relationship between sets. It consists of one or more circles that overlap or intersect, with each circle representing a specific set. The overlapping regions show where sets have elements in common, while the non-overlapping parts display elemenRead more
A Venn diagram is a visual tool used to represent the relationship between sets. It consists of one or more circles that overlap or intersect, with each circle representing a specific set. The overlapping regions show where sets have elements in common, while the non-overlapping parts display elements unique to each set. The circles are enclosed inside a rectangle which represents the universal set.
For example, consider the universal set containing positive integers less than 10, and consider two sets: Set A, which contains even numbers, and Set B, which contains multiples of 3.
A Venn diagram for these sets would have one circle representing even numbers and another circle representing multiples of 3. The overlapping section would represent numbers that are both even and multiples of 3, which in this case is 6. The other numbers that are neither even numbers nor multiples of 3 are placed within the rectangle but outside the circles.

See less