





Lost your password? Please enter your email address. You will receive a link and will create a new password via email.
Please briefly explain why you feel this question should be reported.
Please briefly explain why you feel this answer should be reported.
Please briefly explain why you feel this user should be reported.
Simplify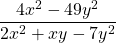
$\dfrac{4x^{2}-49y^{2}}{2x^{2}+xy-7y^{2}}$ The numerator is difference of two squares $\therefore 4x^{2}-49y^{2}=(2x)^{2}-(7y)^{2}=(2x-7y)(2x+7y)$ The denominator is a quadratic equation but it can not be factorized $\therefore \dfrac{4x^{2}-49y^{2}}{2x^{2}+xy-7y^{2}}=\dfrac{(2x-7y)(2x+7y)}{2x^{2}+xRead more
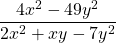
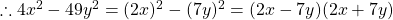
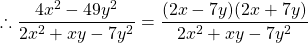
See lessThe numerator is difference of two squares
The denominator is a quadratic equation but it can not be factorized
The probability of obtaining an odd number in a single toss of a fair die is what?
Sample space=$(1,2,3,4,5,6)$ odd numbers=${1,3,5}$ $\therefore$ P(odd numbers)=$\dfrac{3}{6}=\dfrac{1}{2}$
Sample space=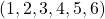
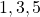
 P(odd numbers)=
P(odd numbers)=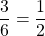
See lessodd numbers=
What is the propability of obtaining a odd number in a single toss of a fair die?
Sample space=$(1,2,3,4,5,6)$ odd numbers=${1,3,5}$ $\therefore$ P(odd numbers)=$\dfrac{3}{6}=\dfrac{1}{2}$
Sample space=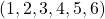
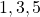
 P(odd numbers)=
P(odd numbers)=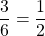
See lessodd numbers=
What is the propability of obtaining a prime number in a single toss of a fair die?
Sample space=$(1,2,3,4,5,6)$ Prime numbers=${2,3,5}$ $\therefore$ P(Prime numbers)=$\dfrac{3}{6}=\dfrac{1}{2}$
Sample space=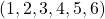
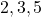
 P(Prime numbers)=
P(Prime numbers)=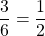
See lessPrime numbers=
What is the propability of obtaining a multiple of 2 in a single toss of a fair die?
Sample space=${1,2,3,4,5,6}$ multiples of 2=${2,4,6}$ $\therefore$ P(multiples of 2)=$\dfrac{3}{6}=\dfrac{1}{2}$
Sample space=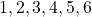
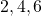
 P(multiples of 2)=
P(multiples of 2)=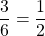
See lessmultiples of 2=
The propability that a number selected at random from 1 to 40 is a multiple of 7 is?
Sample space=${1,2,3,4,5,6...40}$ multiple of 7 within 1 and 40=${7,14,21,28,35}$ $\therefore$ P(multiple of 7)=$\dfrac{5}{40}=\dfrac{1}{8}$
Sample space=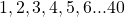
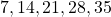
 P(multiple of 7)=
P(multiple of 7)=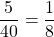
See lessmultiple of 7 within 1 and 40=