Solve the following by using rational algebraic expressions.
Aa_yangaTyro






Lost your password? Please enter your email address. You will receive a link and will create a new password via email.
Please briefly explain why you feel this question should be reported.
Please briefly explain why you feel this answer should be reported.
Please briefly explain why you feel this user should be reported.
a number = x
thrice another number = 3x
the sum of their reciprocal is equal to 4
1/x + 1/3x = 4
LCD = 3x
3x (1/x + 1/3x = 4)
3x/x + 3x/3x = 3x(4)
3 + 1 = 12x
4 = 12x
4/12 = x
1/3 = x
Let the first number be , then the other number is
, then the other number is 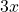 and their reciprocals are
and their reciprocals are  and
and 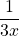 .
.
Thus,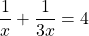 .
.
Multiplying through by the Least Common Denominator (LCD), which is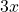 , we have
, we have 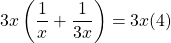
Thus, the first number is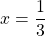 and the other number is
and the other number is 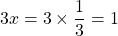 .
.
Therefore, the numbers are and 1.
and 1.