Differentiate ![]() wrt x
wrt x






Lost your password? Please enter your email address. You will receive a link and will create a new password via email.
Please briefly explain why you feel this question should be reported.
Please briefly explain why you feel this answer should be reported.
Please briefly explain why you feel this user should be reported.
Let
and
To differentiate the function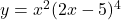 with respect to
with respect to  , you use the product rule.
, you use the product rule.
The product rule states that if you have a function of the form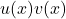 , the derivative is given by:
, the derivative is given by:
In this case, let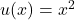 and
and 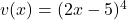 .
.
Now, we’ll find their derivatives:
To find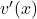 , we’ll need to use the chain rule. The chain rule states that if you have a composite function, such as
, we’ll need to use the chain rule. The chain rule states that if you have a composite function, such as 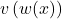 , the derivative of
, the derivative of 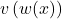 with respect to
with respect to  is given by:
is given by:
Let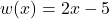 , so
, so 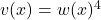 . Now, we can find
. Now, we can find 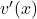 :
:
So,
Now, we can apply the product rule:
Now, simplify this expression:
So, the corrected derivative of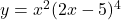 with respect to
with respect to  is:
is: