Home> Questions>Q 4492
Next
Answered

AcedStudy Latest Questions

acedstud
  • 0
Asked: 2021-03-28T18:53:09+00:00 In: ,

Question of the Day (28/03/2021)

  • 0

A language institute teaches three foreign languages, French, Spanish, and Chinese to its enrollees.

In its latest enrollment, 70 people registered. 38 registered for French, 46 registered for Spanish, and 59 registered for Chinese.

If 25 registered for French and Spanish, 38 registered for Chinese and French, and 41 registered for Spanish and Chinese, how many registered for the three languages?

complement of setsintersection of setssetset theoryvenn diagram

You must login to add an answer.

Need An Account,

1 Answer

  2. acedstud
    Best Answer

    First, let us represent the information in a ven diagram for better understanding.

    Since we have three languages, we will have three intersecting circles. Let the circle labeled F, S, and C represent the people that enrolled in French, Spanish, and Chinese. Also, let x represent the number of people that enrolled for the three languages, then:

    The number of people that registered for French and Spanish only is given by 25-x.

    The number of people that registered for French and Chinese only is given by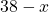 38-x.

    And the number of people that registered for Chinese and Spanish only is given by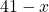 41-x.

    The information is represented in the attached Venn diagram.

    Since a total of 70 people enrolled, the sum of all the parts of the Venn diagram will give us 70.

    Thus,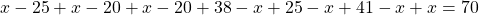 x-25+x-20+x-20+38-x+25-x+41-x+x=70

    \Rightarrow39+x=70

    \Rightarrow x=70-39=31

    Therefore, 31 people enrolled in the three languages.

    Attachment

Related Questions