Home> acedstud>Answers
  1. Asked: October 25, 2023In:

    A __________(Venn diagram, line plot) shows the relationship between sets.

    acedstud
    Best Answer
    acedstud
    This answer was edited.

    A Venn diagram is a visual tool used to represent the relationship between sets. It consists of one or more circles that overlap or intersect, with each circle representing a specific set. The overlapping regions show where sets have elements in common, while the non-overlapping parts display elemenRead more

    A Venn diagram is a visual tool used to represent the relationship between sets. It consists of one or more circles that overlap or intersect, with each circle representing a specific set. The overlapping regions show where sets have elements in common, while the non-overlapping parts display elements unique to each set. The circles are enclosed inside a rectangle which represents the universal set.

    For example, consider the universal set containing positive integers less than 10, and consider two sets: Set A, which contains even numbers, and Set B, which contains multiples of 3.

    A Venn diagram for these sets would have one circle representing even numbers and another circle representing multiples of 3. The overlapping section would represent numbers that are both even and multiples of 3, which in this case is 6. The other numbers that are neither even numbers nor multiples of 3 are placed within the rectangle but outside the circles.

    See less
  2. Asked: September 23, 2021In:

    Multiplying polynomials

    acedstud
    Best Answer
    acedstud

    Multiply two at a time using the distributive property (foil). Multiply $(x^4+3x^2-1)(4x^3+x^2-x+3)=x^4(4x^3+x^2-x+3)+3x^2(4x^3+x^2-x+3)-(4x^3+x^2-x+3)$ $=4x^{4+3}+x^{4+2}-x^{4+1}+3x^4+12x^{2+3}+3x^{2+2}-3x^{2+1}+9x^2-4x^3-x^2+x-3$ $=4x^7+x^6-x^5+3x^4+12x^5+3x^4-3x^3+9x^2-4x^3-x^2+x-3$ Collect likeRead more

    Multiply two at a time using the distributive property (foil).

    Multiply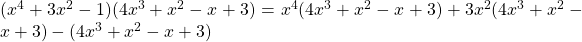 (x^4+3x^2-1)(4x^3+x^2-x+3)=x^4(4x^3+x^2-x+3)+3x^2(4x^3+x^2-x+3)-(4x^3+x^2-x+3)

    =4x^{4+3}+x^{4+2}-x^{4+1}+3x^4+12x^{2+3}+3x^{2+2}-3x^{2+1}+9x^2-4x^3-x^2+x-3

    =4x^7+x^6-x^5+3x^4+12x^5+3x^4-3x^3+9x^2-4x^3-x^2+x-3

    Collect like terms; terms with the same exponent:

    =4x^7+x^6+11x^5+6x^4-7x^3+8x^2+x-3

    Now, multiply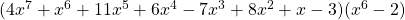 (4x^7+x^6+11x^5+6x^4-7x^3+8x^2+x-3)(x^6-2)

    =x^6(4x^7+x^6+11x^5+6x^4-7x^3+8x^2+x-3)-2(4x^7+x^6+11x^5+6x^4-7x^3+8x^2+x-3)

    =4x^{6+7}+x^{6+6}+11x^{6+5}+6x^{6+4}-7x^{6+3}+8x^{6+2}+x^{6+1}-3x^6-8x^7-2x^6-22x^5-12x^4+14x^3-16x^2-2x+6

    =4x^{13}+x^{12}+11x^{11}+6x^{10}-7x^{9}+8x^{8}+x^{7}-3x^6-8x^7-2x^6-22x^5-12x^4+14x^3-16x^2-2x+6

    Collect like terms; terms with the same exponent

    4x^{13}+x^{12}+11x^{11}+6x^{10}-7x^{9}+8x^{8}-7x^{7}-5x^6-22x^5-12x^4+14x^3-16x^2-2x+6

    See less
  3. Asked: May 20, 2021In: ,

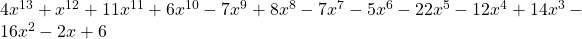
    Solids for which Volume = 1/3 Bh

    acedstud
    acedstud
    This answer was edited.

    The frustum of a solid is the portion of the solid that lies between one or two parallel planes cutting it. Given that the lower base is an equilateral triangle with an edge of 9 m, thus, the area of the lower base is $B=\dfrac{1}{2}\times9\times9\times\sin{60^o}\approx35.074$ m$^2$. Let the lengthRead more

    The frustum of a solid is the portion of the solid that lies between one or two parallel planes cutting it.

    Given that the lower base is an equilateral triangle with an edge of 9 m, thus, the area of the lower base is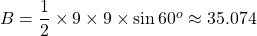 B=\dfrac{1}{2}\times9\times9\times\sin{60^o}\approx35.074 m^2.

    Let the length of the upper base be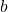 b, and the height of the cut-off pyramid be 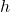h, then given that the upper base is 8 m above the lower base, i.e. H-h=8\Rightarrow H=h+8.

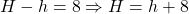    Since the pyramid is regular, thus the bottom and top of the frustum are equilateral triangles (they are similar). This means that by the polygons similarity rules, the proportion of the heights of the cut-off pyramid and the entire pyramid is equal to the proportion of the lengths of the base edges.

    Thus,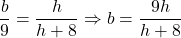 \dfrac{b}{9}=\dfrac{h}{h+8}\Rightarrow b=\dfrac{9h}{h+8}, where 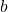b is the length of the edge of the top base.

    The area of the base of the cut-off pyramid (the top base of the frustum) is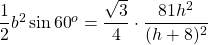 \dfrac{1}{2}b^2\sin{60}^o=\dfrac{\sqrt{3}}{4}\cdot\dfrac{81h^2}{(h+8)^2}.

    The volume of the frustum of a triangular pyramid is given by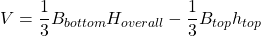 V=\dfrac{1}{3}B_{bottom}H_{overall}-\dfrac{1}{3}B_{top}h_{top}, where 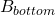B_{bottom} is the area of the lower base, 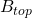B_{top} is the area of the upper base, 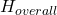H_{overall} is the height of the original pyramid and 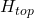H_{top} is the height of the cut off upper pyramid.

    Thus,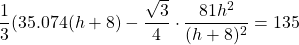 \dfrac{1}{3}(35.074(h+8)-\dfrac{\sqrt{3}}{4}\cdot\dfrac{81h^2}{(h+8)^2}=135

    \Rightarrow35.074h+280.592-\dfrac{\sqrt{3}}{4}\cdot\dfrac{81h^2}{(h+8)^2}=3\times135=405

    Multiplying through by the denominator, gives

    \Rightarrow140.296h(h+8)^2+1122.368(h+8)^2-81\sqrt{3}h^3=1620(h+8)^2.

    \Rightarrow140.296h(h^2+16h+64)+1122.368(h^2+16h+64)-140.296h^3=1620(h^2+16h+64).

    \Rightarrow140.296h^3+2244.736h^2+8978.944h+1122.368h^2+17957.888h+71831.552-140.296h^3=1620h^2+25920h+103680.

    \Rightarrow1747.104h^2+1016.832h-31848.448=0.

    Solving the quadratic equation gives that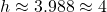 h\approx3.988\approx4.

    Substituting for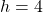 h=4 into the equation for b, gives that b=\dfrac{9(4)}{4+8}=\dfrac{36}{12}=3.

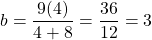    Therefore,  the length of the top edge of the frustum is 3 m.

    See less
  4. Asked: May 6, 2021In: ,

    Find the angle between the normals to the surface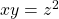 xy=z^2 at (1, 4, 2) and (-3, -3, 3)

    acedstud
    acedstud
    This answer was edited.

    First, we express the curve in the form $F(x, y, z) = c$, where $c$ is a constant. Thus, $F(x, y, z) = xy - z^2 = 0$ Next, we find the normal vector to $F$, which is the gradient of $F$, that is $\nabla{F}$. Thus, $\nabla{F}=\left(\dfrac{\partial}{\partial{x}}i+\dfrac{\partial}{\partial{y}}j+\dfrac{Read more

    First, we express the curve in the form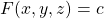 F(x, y, z) = c, where c is a constant.

    Thus,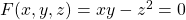 F(x, y, z) = xy - z^2 = 0

    Next, we find the normal vector to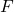 F, which is the gradient of 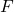F, that is \nabla{F}.

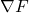    Thus,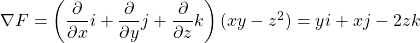 \nabla{F}=\left(\dfrac{\partial}{\partial{x}}i+\dfrac{\partial}{\partial{y}}j+\dfrac{\partial}{\partial{z}}k\right)(xy-z^2)=yi+xj-2zk.

    The normal vector at (1, 4, 2) is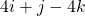 4i+j-4k, and the normal vector at (-3, -3, 3) is -3i-3j-6k.

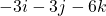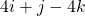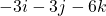    Finally, the angle between the two vectors 4i+j-4k and -3i-3j-6k is given by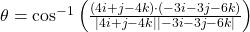 \theta=\cos^{-1}\left(\frac{(4i+j-4k)\cdot(-3i-3j-6k)}{|4i+j-4k||-3i-3j-6k|}\right)

    =\cos^{-1}\left(\frac{9}{\sqrt{33}\times\sqrt{54}}\right)=\cos^{-1}(0.2132)\approx77.7^o.

    Therefore, the angle between the normals to the surface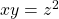 xy=z^2 at (1, 4, 2) and (-3, -3, 3) is approximately 77.7^o.

    See less
  5. Asked: May 6, 2021In: ,

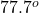    Find the radius and volume of a cylinder

    acedstud
    acedstud

    First, let us assume that the cylinder is closed at both ends, then the total surface area of the cylinder is given by $S=2\pi r^2+2\pi rh$, where $r$ and $h$ are the radius and the height of the cylinder respectively. Given that the surface area is $78\pi$ and the height is 10, we have $78\pi=2\piRead more

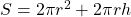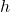    First, let us assume that the cylinder is closed at both ends, then the total surface area of the cylinder is given by S=2\pi r^2+2\pi rh, where r and h are the radius and the height of the cylinder respectively.

    Given that the surface area is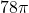 78\pi and the height is 10, we have

    78\pi=2\pi r^2+2\pi r(10)=2\pi(r^2+10r)

    Dividing both sides by 2, we have

    39=r^2+10r\Rightarrow r^2+10r-39=0\Rightarrow(r-3)(r+13)=0\Rightarrow r-3=0 or r+13=0\Rightarrow r=3 or r=-13, but radius cannot be negative, so r=3.

    Therefore, the radius is 3.

     

    The volume of a cylinder is given by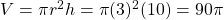 V=\pi r^2h=\pi(3)^2(10)=90\pi.

    Therefore, the volume of the cylinder is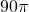 90\pi.

    See less
  6. Asked: April 22, 2021In:

    Evaluate the following combinations

    acedstud
    Best Answer
    acedstud

    The combination of n objects taking r at a time is given by C(n, r) = $\dfrac{n!}{r!(n-r)!}$. Thus, $C(4, 2)=\dfrac{4!}{2!(4-2)!}=\dfrac{4!}{2!2!}=\dfrac{4\times3\times2\times1}{2\times1\times2\times1}$ $=3\times2=6$ Therefore, 2C(4, 2) - 10 = 2(6) - 10 = 12 - 10 = 2.

    The combination of n objects taking r at a time is given by C(n, r) =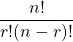 \dfrac{n!}{r!(n-r)!}.

    Thus,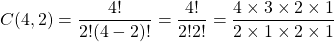 C(4, 2)=\dfrac{4!}{2!(4-2)!}=\dfrac{4!}{2!2!}=\dfrac{4\times3\times2\times1}{2\times1\times2\times1}

    =3\times2=6

    Therefore, 2C(4, 2) – 10 = 2(6) – 10 = 12 – 10 = 2.

    See less
  7. Asked: April 17, 2021In: ,

    24×2+25x−47 ax−2 =−8x−3− 53 ax−2 is true for all values of x≠ 2/a where a is a constant. What is the value of a?

    acedstud
    acedstud

    Hello, your question is not clear enough and I cannot understand the question. Can you please use the question details box to clearly ask your question so that you can get an answer.

    Hello, your question is not clear enough and I cannot understand the question.

    Can you please use the question details box to clearly ask your question so that you can get an answer.

    See less
  8. Asked: April 17, 2021In: ,

    Probabilty of multiple choices

    acedstud
    acedstud

    Since the probability of getting a question wrong is 0.8, then the probability of getting a question right is 1 - 0.8 = 0.2 Then using the binomial probability distribution where number of trials, $n=10$, probability of success, $p=0.2$, then $P(X=x)=^nC_xp^x(1-p)^{n-x}$. Thus, $P(X=5)=^{10}C_5(0.2)Read more

    Since the probability of getting a question wrong is 0.8, then the probability of getting a question right is 1 – 0.8 = 0.2

    Then using the binomial probability distribution where number of trials,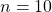 n=10, probability of success, 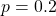p=0.2, then P(X=x)=^nC_xp^x(1-p)^{n-x}.

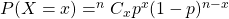    Thus,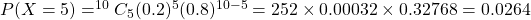 P(X=5)=^{10}C_5(0.2)^5(0.8)^{10-5}=252\times0.00032\times0.32768=0.0264.

    Therefore, the probability of getting 5 questions correct is 0.0264.

    See less
  9. Asked: April 17, 2021In: ,

    multiple choice ( geometry )

    acedstud
    Best Answer
    acedstud

    A square pyramid has a square base and 4 triangular faces which meet at a point, called the vertex. Therefore, a square pyramid has a total of 5 faces.

    A square pyramid has a square base and 4 triangular faces which meet at a point, called the vertex.

    Therefore, a square pyramid has a total of 5 faces.

    See less
    Attachment

  10. Asked: April 17, 2021In: ,

    Normal Distribution

    acedstud
    acedstud

    The area under the standard normal curve between $z=0.75$ and $z=1.04$ is given by $P(z<1.04)-P(z<0.75)$. Using the table of values under the standard normal curve, we have $=0.85083-0.77337=0.07746$.

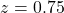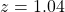    The area under the standard normal curve between z=0.75 and z=1.04 is given by 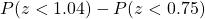P(z<1.04)-P(z<0.75). Using the table of values under the standard normal curve, we have

    =0.85083-0.77337=0.07746.

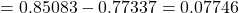    See less