Home> Questions>Q 7629
In Process

AcedStudy Latest Questions

dlcrzngl
  • 0
Tyro
Asked: 2021-05-20T12:56:28+00:00 In: ,

Solids for which Volume = 1/3 Bh

  • 0

The volume of the frustum of a regular
triangular pyramid is 135 cu.m. The lower
base is an equilateral triangle with an edge
of 9 cm. The upper base is 8 m above the
lower base. What is the upper base edge in
meters?

solution

You must login to add an answer.

Need An Account,

1 Answer

  2. acedstud
    This answer was edited.

    The frustum of a solid is the portion of the solid that lies between one or two parallel planes cutting it.

    Given that the lower base is an equilateral triangle with an edge of 9 m, thus, the area of the lower base is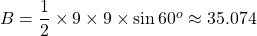 B=\dfrac{1}{2}\times9\times9\times\sin{60^o}\approx35.074 m^2.

    Let the length of the upper base be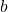 b, and the height of the cut-off pyramid be 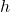h, then given that the upper base is 8 m above the lower base, i.e. H-h=8\Rightarrow H=h+8.

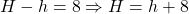    Since the pyramid is regular, thus the bottom and top of the frustum are equilateral triangles (they are similar). This means that by the polygons similarity rules, the proportion of the heights of the cut-off pyramid and the entire pyramid is equal to the proportion of the lengths of the base edges.

    Thus,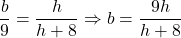 \dfrac{b}{9}=\dfrac{h}{h+8}\Rightarrow b=\dfrac{9h}{h+8}, where 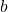b is the length of the edge of the top base.

    The area of the base of the cut-off pyramid (the top base of the frustum) is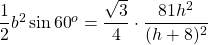 \dfrac{1}{2}b^2\sin{60}^o=\dfrac{\sqrt{3}}{4}\cdot\dfrac{81h^2}{(h+8)^2}.

    The volume of the frustum of a triangular pyramid is given by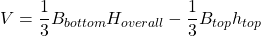 V=\dfrac{1}{3}B_{bottom}H_{overall}-\dfrac{1}{3}B_{top}h_{top}, where 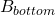B_{bottom} is the area of the lower base, 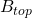B_{top} is the area of the upper base, 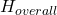H_{overall} is the height of the original pyramid and 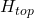H_{top} is the height of the cut off upper pyramid.

    Thus,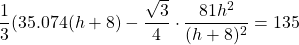 \dfrac{1}{3}(35.074(h+8)-\dfrac{\sqrt{3}}{4}\cdot\dfrac{81h^2}{(h+8)^2}=135

    \Rightarrow35.074h+280.592-\dfrac{\sqrt{3}}{4}\cdot\dfrac{81h^2}{(h+8)^2}=3\times135=405

    Multiplying through by the denominator, gives

    \Rightarrow140.296h(h+8)^2+1122.368(h+8)^2-81\sqrt{3}h^3=1620(h+8)^2.

    \Rightarrow140.296h(h^2+16h+64)+1122.368(h^2+16h+64)-140.296h^3=1620(h^2+16h+64).

    \Rightarrow140.296h^3+2244.736h^2+8978.944h+1122.368h^2+17957.888h+71831.552-140.296h^3=1620h^2+25920h+103680.

    \Rightarrow1747.104h^2+1016.832h-31848.448=0.

    Solving the quadratic equation gives that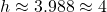 h\approx3.988\approx4.

    Substituting for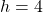 h=4 into the equation for 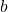b, gives that b=\dfrac{9(4)}{4+8}=\dfrac{36}{12}=3.

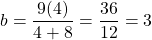    Therefore,  the length of the top edge of the frustum is 3 m.

Related Questions