





Lost your password? Please enter your email address. You will receive a link and will create a new password via email.
Please briefly explain why you feel this question should be reported.
Please briefly explain why you feel this answer should be reported.
Please briefly explain why you feel this user should be reported.
Question of the Day (22/03/2021)
Let $X$ be a random variable representing the number of accidents that occur on the stretch of the road in a certain month, then since $X$ follows a Poisson distribution, $P(X=x)=\dfrac{\lambda^xe^{-\lambda}}{x!}$, where $x=0,1,2,3,...; \lambda$ is the average number of accidents on the road per monRead more
Let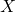 be a random variable representing the number of accidents that occur on the stretch of the road in a certain month, then since
be a random variable representing the number of accidents that occur on the stretch of the road in a certain month, then since 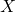 follows a Poisson distribution,
follows a Poisson distribution, 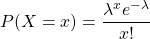 , where
, where 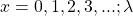 is the average number of accidents on the road per month and
is the average number of accidents on the road per month and  is the exponential constant which is approximately 2.71828.
is the exponential constant which is approximately 2.71828.
a.) Given: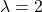
(i)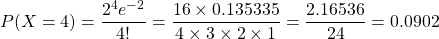
(ii) The probability of at least 1 accident means the probability of 1 or more accidents. That is,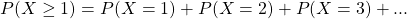 . Using the compliment law of probabilities, we have
. Using the compliment law of probabilities, we have 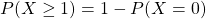 .
.
Therefore,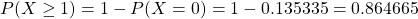
b.) Since the average number (expected number) of accidents per month is 2, the expected number of accidents in three months is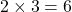 accidents.
accidents.
c.) Let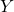 be a random variable representing the number of accidents that occur on the stretch of the road in a certain three months. In three months, the average number (expected number) of accidents is 6, so
be a random variable representing the number of accidents that occur on the stretch of the road in a certain three months. In three months, the average number (expected number) of accidents is 6, so 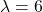
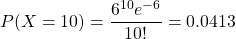
See lessThe demand equations for related products A and B are given by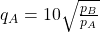 …
…
i.) Given: $q_A=10\sqrt{\dfrac{P_B}{P_A}}=10P_B^{\frac{1}{2}}P_A^{-\frac{1}{2}}$; $\dfrac{dq_A}{dP_A}=-\dfrac{1}{2}\cdot10P_B^{\frac{1}{2}}P_A^{-\frac{3}{2}}=-5P_B^{\frac{1}{2}}P_A^{-\frac{3}{2}}$ When $P_A=9$, and $P_B=16$: $\dfrac{dq_A}{dP_A}=-5\times(16)^{\frac{1}{2}}(9)^{-\frac{3}{2}}=-5\times4\Read more
i.) Given: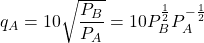 ;
;
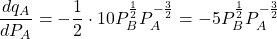
When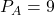 , and
, and 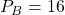 :
:
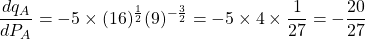
Given:![Rendered by QuickLaTeX.com q_B=3\sqrt[3]{\dfrac{P_A}{P_B}}=3P_A^{\frac{1}{3}}P_B^{-\frac{1}{3}}](https://acedstudy.com/wp-content/ql-cache/quicklatex.com-d45124e22482121f7a0e001284680ea0_l3.png)
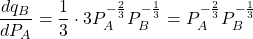
When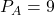 , and
, and 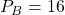 :
:
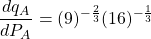
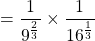
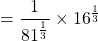
![Rendered by QuickLaTeX.com =\sqrt[3]{\dfrac{1}{81\times16}}=\sqrt[3]{\dfrac{1}{1296}}\approx0.09172](https://acedstudy.com/wp-content/ql-cache/quicklatex.com-0c1e9edca6555075f6317f19f34ab453_l3.png)
ii.)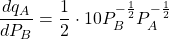
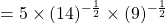
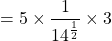
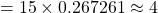
See lessQuestion of the Day (16/03/2021)
Given that the relationship between the amount spent, A, and the number of hours, h, is $A=9h+13$. Given that he spent \$238 last month, that is $A=\$238$. Thus, $238=9h+13$ Subtracting 13 from both sides, we have: $238 - 13 = 9h + 13 - 13 \Rightarrow 225 = 9h$ Dividing both sides by 9, we have: $\dRead more
Given that the relationship between the amount spent, A, and the number of hours, h, is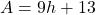 .
.
Given that he spent $238 last month, that is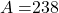 .
.
Thus,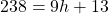
Subtracting 13 from both sides, we have:
Dividing both sides by 9, we have:
Therefore, Edward spent 25 hours exercising at the gym last month.
See lessQuestion of the Day (15/03/2021)
The volume of the box is the sum of the volumes of the rectangular prism (cuboid) and the triangular prism. Volume of the rectangular prism = length $\times$ width $\times$ height $=18\times7\times2=252 \text{in}^3$. Volume of the triangular prism = $\dfrac{1}{2}\times$ length $\times$ width $\timesRead more
The volume of the box is the sum of the volumes of the rectangular prism (cuboid) and the triangular prism.
Volume of the rectangular prism = length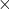 width
width 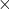 height
height 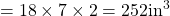 .
.
Volume of the triangular prism =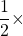 length
length 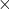 width
width 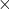 height
height 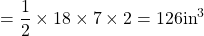 .
.
Volume of the box = Volume of the rectangular prism + Volume of the triangular prism =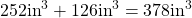 .
.
See lessQuestion of the Day (14/03/2021)
First, we find the slope of the tangent line by finding the derivative of $f(x)$ at $x=-1$. Given: $f(x)=-3x-x^4$. Then, $f'(x)=-3-4x^3$ and $f'(-1)=-3-4(-1)^3=-3-4(-1)=-3+4=1$. Thus, the slope of the tangent line is 1. Next, we find the y-coordinate of the function $f(x)$ at $x=-1$. At $x=-1, y=f(-Read more
First, we find the slope of the tangent line by finding the derivative of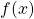 at
at 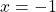 .
.
Given: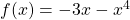 .
.
Then,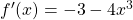 and
and 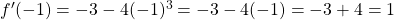 .
.
Thus, the slope of the tangent line is 1.
Next, we find the y-coordinate of the function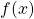 at
at 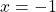 .
.
At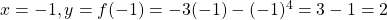 .
.
Thus, the point of tangency is (-1, 2).
Finally, the equation of a line with a slope of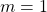 and passing through the point
and passing through the point 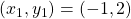 is given as follows:
is given as follows:
Therefore, the required equation is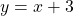 .
.
See lessQuestion of the Day (10/03/2021)
We can solve this question by evaluating the option. Option A: 67 + 31 = 98. (Not correct) Option B: 31 + 16 = 47. (Not correct) Option C: 13 + 68 = 81. (Correct) Option D: 24 + 81 = 105. (Not correct) There option C (13 + 68) will give 81, and hence, the correct answRead more
We can solve this question by evaluating the option.
Option A:
67 + 31 = 98. (Not correct)
Option B:
31 + 16 = 47. (Not correct)
Option C:
13 + 68 = 81. (Correct)
Option D:
24 + 81 = 105. (Not correct)
There option C (13 + 68) will give 81, and hence, the correct answer.
See lessQuestion of the Day (09/03/2021)
A term is a single number or variable or a product of number(s) and variables(s) in a mathematical expression or equation, separated by + or - signs. Given $4+5x^4+x^3+7x^2-7$. Simplifying the like terms gives: $5x^4+x^3+7x^2-3$. Thus, there are 4 terms after simplification. Therefore, the number ofRead more
A term is a single number or variable or a product of number(s) and variables(s) in a mathematical expression or equation, separated by + or – signs.
Given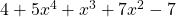 .
.
Simplifying the like terms gives: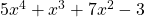 .
.
Thus, there are 4 terms after simplification.
Therefore, the number of terms is 4.
See lessQuestion of the Day (08/03/2021)
Since the roots are at $x=1$ and $x=-17$, the equation is of the form $y=a(x-1)(x+17)$ . . . . . . . .(1) Also, since the vertex of the graph is at the point (-8, -81), the vertex form of the quadratic equation is $y=a(x+8)^2-81$ . . . . . . . .(2) Equating equation (1) and (2) gives: $a(x-1)(x+17)=Read more
Since the roots are at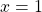 and
and 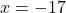 , the equation is of the form
, the equation is of the form 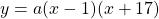 . . . . . . . .(1)
. . . . . . . .(1)
Also, since the vertex of the graph is at the point (-8, -81), the vertex form of the quadratic equation is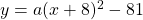 . . . . . . . .(2)
. . . . . . . .(2)
Equating equation (1) and (2) gives:
Substituting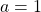 into equation (1) gives:
into equation (1) gives:
Therefore,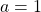 ,
, 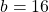 , and
, and 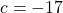 .
.
See lessWrite the equation of a line if the gradient is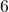 and the y-intercept is
and the y-intercept is 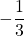
The equation of a line is given by $y=mx+c$; where $m$ is the slope or gradient, and $c$ is the y-intercept. Given: $m=6$ and $c=-\dfrac{1}{3}$ Therefore, the required equation is $y=6x-\dfrac{1}{3}$.
The equation of a line is given by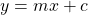 ; where
; where 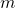 is the slope or gradient, and
is the slope or gradient, and  is the y-intercept.
is the y-intercept.
Given: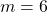 and
and 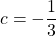
Therefore, the required equation is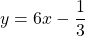 .
.
See lessAt what rate of simple interest will $500 accumulate to $615 in 2.5 years?
This question deal with simple interest. The total amount (A) accumulated in simple interest after t years is given by $A=P(1+rt)$, where P is the principal. Given: $P=\$500$, $A=\$615$, $t=2.5$ years. Substituting for $P$, $A$, and $t$, into the formula $A=P(1+rt)$, we have: $615=500(1+2.5r)$ DividRead more
This question deal with simple interest.
The total amount (A) accumulated in simple interest after t years is given by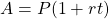 , where P is the principal.
, where P is the principal.
Given: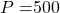 ,
, 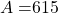 ,
, 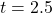 years.
years.
Substituting for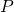 ,
, 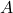 , and
, and 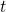 , into the formula
, into the formula 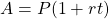 , we have:
, we have:
Dividing both sides by 500 we have:
Subtracting 1 from both sides, we have:
Dividing both sides by 2.5, we have:
Therefore, the rate is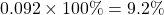 .
.
See less