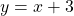Find the equation of the tangent line to the curve ![]() at
at ![]() .
.






Lost your password? Please enter your email address. You will receive a link and will create a new password via email.
Please briefly explain why you feel this question should be reported.
Please briefly explain why you feel this answer should be reported.
Please briefly explain why you feel this user should be reported.
First, we find the slope of the tangent line by finding the derivative of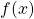 at
at 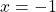 .
.
Given: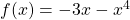 .
.
Then,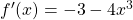 and
and 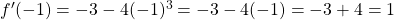 .
.
Thus, the slope of the tangent line is 1.
Next, we find the y-coordinate of the function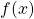 at
at 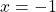 .
.
At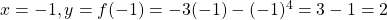 .
.
Thus, the point of tangency is (-1, 2).
Finally, the equation of a line with a slope of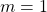 and passing through the point
and passing through the point 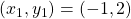 is given as follows:
is given as follows:
Therefore, the required equation is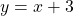 .
.
We know that the equation of a tangent line of the curve on a function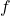 at the point
at the point 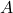 with abscissa
with abscissa 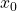 is
is 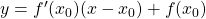 , in our case
, in our case 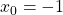 , so the equation is
, so the equation is 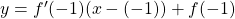
So let’s calculate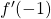 and
and 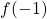 .
.
We have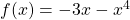
Thus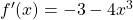
Then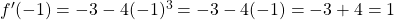
And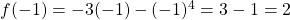
Therefore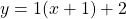
Finaly