





Lost your password? Please enter your email address. You will receive a link and will create a new password via email.
Please briefly explain why you feel this question should be reported.
Please briefly explain why you feel this answer should be reported.
Please briefly explain why you feel this user should be reported.
Find the value of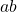 if
if 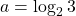 and
and 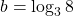
$a=\log_{2}3$ and $b=\log_{8}3$ $a=\log_{2}3=\log 3\div \log 2$ $b=\log_{3}8=\log 8\div \log 3$ $ab=\dfrac{\log 3}{\log 2}\times \dfrac{\log 8}{\log 3}$ $ab=\dfrac{\log 8}{\log 2}$ $ab=\dfrac{\log 2^{3}}{\log 2}$ $ab=\dfrac{3\log 2}{\log 2}=3$
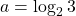 and
and 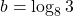
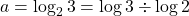
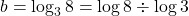
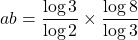
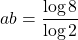
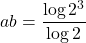
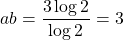
See lessFind the derivative of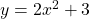
$y=2x^{2}+3$ $\dfrac{dy}{dx}=2\times 2x^{2-1}+0$ $\dfrac{dy}{dx}=4x^{1}$ $\dfrac{dy}{dx}=4x$
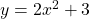
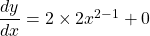
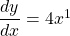
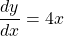
See lessFind the derivative of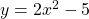
$y=2x^{2}-5$ $\dfrac{dy}{dx}=2\times 2x^{2-1}-0$ $\dfrac{dy}{dx}=4x^{1}$ $\dfrac{dy}{dx}=4x$
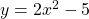
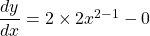
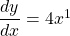
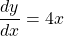
See lessFind the derivative of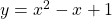
$y=x^{2}-x+1$ $\dfrac{dy}{dx}=2\times x^{2-1}-1\times x^{1-1}+0$ $\dfrac{dy}{dx}=2x^{1}-x^{0}$ $\dfrac{dy}{dx}=2x-1$
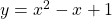
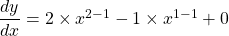
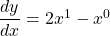
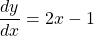
See lessIf angle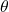 is
is 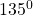 , evaluate
, evaluate 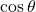
$\cos 135^{0}$ $135$ can be found in the second quadrant and cosine is negative there $\cos 135^{0}=-\cos (180^{0}-135^{0})$ $\Rightarrow -\cos 45^{0}=-\frac{\sqrt{2}}{2}=0.7071$
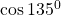
 can be found in the second quadrant and cosine is negative there
can be found in the second quadrant and cosine is negative there
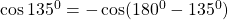
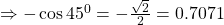
See lessGiven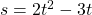 , find
, find 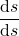
$s=2t^{2}-3t$ $\dfrac{ds}{dt}=2\times 2t^{2-1}-1\times 3t^{1-1}$ $\dfrac{ds}{dt}=4t^{1}-3t^{0}$ $\dfrac{ds}{dt}=4t-3$
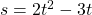
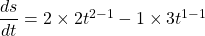
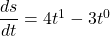
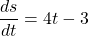
See lessGiven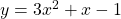 , find
, find 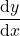
$y=3x^{2}+x-1$ $\dfrac{dy}{dx}=2\times 3x^{2-1}+1\times x^{1-1}-0$ $\dfrac{dy}{dx}=6x^{1}+x^{0}$ $\dfrac{dy}{dx}=6x+1$
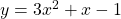
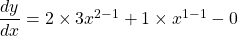
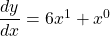
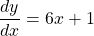
See lessDifferentiate with respect to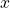 :
: 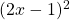
$y=(2x-1)^{2}$ Let $u=2x-1$ and $y=u^{2}$ $\dfrac{du}{dx}=2$ and $\dfrac{dy}{du}=2u$ $\dfrac{dy}{dx}=\dfrac{du}{dx}\times \dfrac{dy}{du}$ $\dfrac{dy}{dx}=2\times 2u$ $\dfrac{dy}{dx}=4u$ $\dfrac{dy}{dx}=4(2x-1)=8x-4$
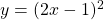
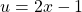 and
and 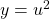
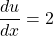 and
and 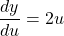
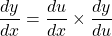
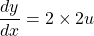
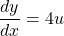
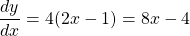
See lessLet
Find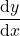 if
if 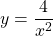
$y=4x^{-2}$ $\dfrac{dy}{dx}=-2\times 4x^{-2-1}$ $\dfrac{dy}{dx}=-8x^{-3}$ $\dfrac{dy}{dx}=-\dfrac{8}{x^{3}}$
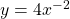
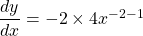
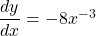
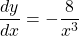
See lessFind the derivative of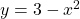
$y=3-x^{2}$ $\dfrac{dy}{dx}=0-2\times x^{2-1}$ $\dfrac{dy}{dx}=0+x^{0}-2x^{1}$ $\dfrac{dy}{dx}=1-2x$
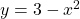
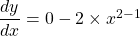
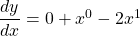
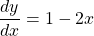
See less