





Lost your password? Please enter your email address. You will receive a link and will create a new password via email.
Please briefly explain why you feel this question should be reported.
Please briefly explain why you feel this answer should be reported.
Please briefly explain why you feel this user should be reported.
Find the value of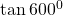
$\tan 600^{0}$ first step is to subtract 360 from the value above $\tan (600^{0}-360^{0})= \tan 240^{0}$ 240 falls in the second quadrant and tangent is positive $\Rightarrow +\tan (240^{0}-180^{0})=\tan 60^{0}$ using table $\therefore \tan 60^{0}=1.732$
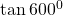
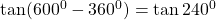
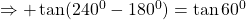
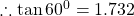
See lessfirst step is to subtract 360 from the value above
240 falls in the second quadrant and tangent is positive
using table
Find the value of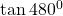
$\tan 480^{0}$ first step is to subtract 360 from the value above $\tan (480^{0}-360^{0})= \tan 120^{0}$ 120 falls in the second quadrant and tangent is negative $-\tan (180^{0}-120^{0})=-\tan 60^{0}$ using table $\therefore -\tan 60^{0}=-1.732$
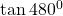
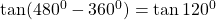
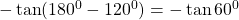
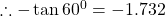
See lessfirst step is to subtract 360 from the value above
120 falls in the second quadrant and tangent is negative
using table
Find the value of
$\cos 540^{0}$ first step is to subtract 360 from the value above $\Rightarrow \cos (540^{0}-360^{0})=\cos 180^{0}$ 180 falls in the second quadrant and cosine is negative $\Rightarrow -\cos (180^{0}-180^{0})=-\cos 0^{0}$ using table $\therefore -\cos 0^{0}=-1$
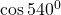
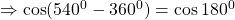
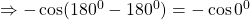
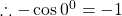
See lessfirst step is to subtract 360 from the value above
180 falls in the second quadrant and cosine is negative
using table
Find the value of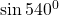
$\sin 540^{0}$ since 540 is bigger than 360, we will subtract 360 from 540 $\sin (540^{0}-360^{0})=\sin (180^{0})$ 180 falls in the second quadrant and sine is positive $+\sin (180^{0}-180^{0})=\sin 0^{0}$ $\therefore \sin 0^{0}=0$
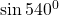
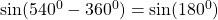
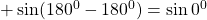
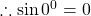
See lesssince 540 is bigger than 360, we will subtract 360 from 540
180 falls in the second quadrant and sine is positive
Find the value of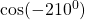
$\cos (-210^{0})=-\cos (210^{0})$ since 210 falls in the third quadrant and cosine is positive $\Rightarrow -(+\cos (210^{0}-180^{0}))$ using table $\therefore -\cos (30^{0})=-0.866$
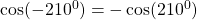
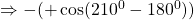
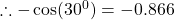
See lesssince 210 falls in the third quadrant and cosine is positive
using table
Find the value of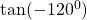
$\tan (-120^{0})=-\tan (120^{0})$ since 120 falls in the second quadrant and tangent is negative $\Rightarrow -(-\tan (180^{0}-120^{0}))$ using four figure table $\therefore \tan 60^{0}=1.732$
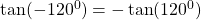
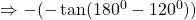
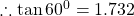
See lesssince 120 falls in the second quadrant and tangent is negative
using four figure table
Find the value of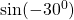
$\sin (-30^{0})=-\sin (30^{0})$ 30 falls on the first quadrant and sine is positive $\therefore -\sin 30^{0}=-0.5$
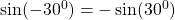
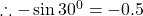
See less30 falls on the first quadrant and sine is positive
Find the value of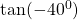
$\tan (-40^{0})=-(\tan40^{0})$ since 40 falls in the first quadrant and tangent is positive $\Rightarrow -(+\tan40^{0})$ using four figure table $\therefore -\tan40^{0}=-0.8391$
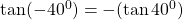
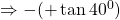
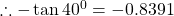
See lesssince 40 falls in the first quadrant and tangent is positive
using four figure table
Find the value of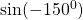
$\sin (-150^{0})=- \sin (150^{0})$ since 150 falls in the second quadrant and sine is positive $-(+\sin (180^{0}-150^{0}))=-(\sin 30^{0})$ using four figure table $\therefore -(\sin 30^{0})=-0.5$
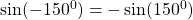
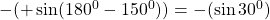
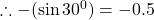
See lesssince 150 falls in the second quadrant and sine is positive
using four figure table
Find the value of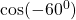
$\cos (-60^{0})=-\cos (60^{0})$ using four figure table $-\cos (60^{0})= -0.5$ or $-\dfrac{1}{2}$
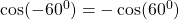
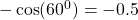 or
or 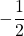
See lessusing four figure table