





Lost your password? Please enter your email address. You will receive a link and will create a new password via email.
Please briefly explain why you feel this question should be reported.
Please briefly explain why you feel this answer should be reported.
Please briefly explain why you feel this user should be reported.
If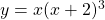 , find
, find 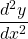
$y=x(x+2)^{3}$ Let $u=x$ and $v=(x+2)^{3}$ $\dfrac{du}{dx}=1$ and $\dfrac{dv}{dx}=3(x+2)^{2}$ $\dfrac{dy}{dx}=v\dfrac{du}{dx}+u\dfrac{dv}{dx}$ $\dfrac{dy}{dx}=(x+2)^{3}\times 1+x\times 3(x+2)^{2}$ $\dfrac{dy}{dx}=(x+2)^{3}+3x(x+2)^{2}$ $\dfrac{dy}{dx}=(x+2)^{2}(x+2+3x)$ $\dfrac{dy}{dx}=(x+2)^{2}(4x+Read more
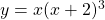
 and
and 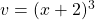
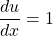 and
and 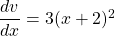
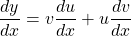
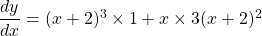
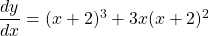
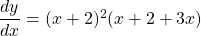
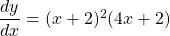
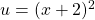 and
and 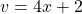
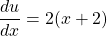 and
and 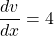
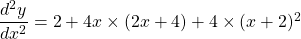
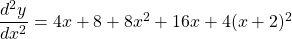
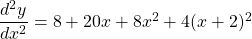
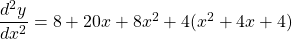
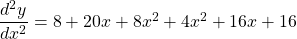
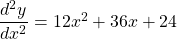
See lessLet
Let
If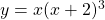 , find
, find 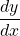
$y=x(x+2)^{3}$ Let $u=x$ and $v=(x+2)^{3}$ $\dfrac{du}{dx}=1$ and $\dfrac{dv}{dx}=3(x+2)^{2}$ $\dfrac{dy}{dx}=v\dfrac{du}{dx}+u\dfrac{dv}{dx}$ $\dfrac{dy}{dx}=(x+2)^{3}\times 1+x\times 3(x+2)^{2}$ $\dfrac{dy}{dx}=(x+2)^{3}+3x(x+2)^{2}$ $\dfrac{dy}{dx}=(x+2)^{2}(x+2+3x)$ $\dfrac{dy}{dx}=(x+2)^{2}(4x+Read more
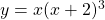
 and
and 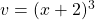
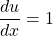 and
and 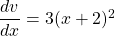
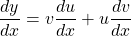
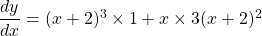
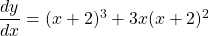
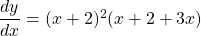
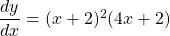
See lessLet
If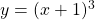 , find
, find 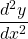
$y=(x+1)^{3}$ Let $u=x+1$ and $y=u^{3}$ $\dfrac{du}{dx}=1$ and $\dfrac{dy}{du}=3u^{2}$ $\dfrac{dy}{dx}=\dfrac{du}{dx}\times \dfrac{dy}{du}$ $\dfrac{dy}{dx}=1\times 3u^{2}$ $\dfrac{dy}{dx}=3xu^{2}=3x(x+1)^{2}$ $\dfrac{d^{2}y}{dx^{2}}=(2x\times 2)\times 3x(x^{2}-1)^{2-1}$ $\dfrac{d^{2}y}{dx^{2}}=12x^{Read more
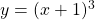
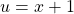 and
and 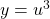
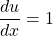 and
and 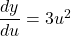
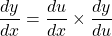
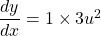
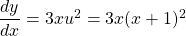
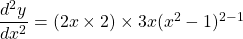
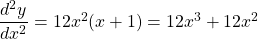
See lessLet
If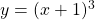 , find
, find 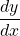
$y=(x+1)^{3}$ Let $u=x+1$ and $y=u^{3}$ $\dfrac{du}{dx}=1$ and $\dfrac{dy}{du}=3u^{2}$ $\dfrac{dy}{dx}=\dfrac{du}{dx}\times \dfrac{dy}{du}$ $\dfrac{dy}{dx}=1\times 3u^{2}$ $\dfrac{dy}{dx}=3xu^{2}=3x(x+1)^{2}$
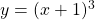
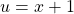 and
and 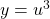
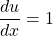 and
and 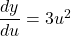
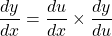
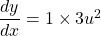
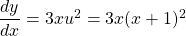
See lessLet
If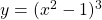 , find
, find 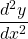
$y=(x^{2}-1)^{3}$ Let $u=x^{2}-1$ and $y=u^{3}$ $\dfrac{du}{dx}=2x$ and $\dfrac{dy}{du}=3u^{2}$ $\dfrac{dy}{dx}=\dfrac{du}{dx}\times \dfrac{dy}{du}$ $\dfrac{dy}{dx}=2x\times 3u^{2}$ $\dfrac{dy}{dx}=6xu^{2}=6x(x^{2}-1)^{2}$ $\dfrac{d^{2}y}{dx^{2}}=(2x\times 2)\times 6x(x^{2}-1)^{2-1}$ $\dfrac{d^{2}y}Read more
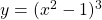
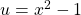 and
and 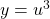
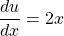 and
and 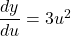
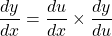
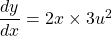
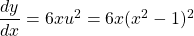
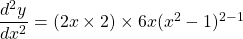
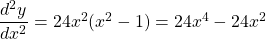
See lessLet
If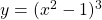 , find
, find 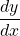
$y=(x^{2}-1)^{3}$ Let $u=x^{2}-1$ and $y=u^{3}$ $\dfrac{du}{dx}=2x$ and $\dfrac{dy}{du}=3u^{2}$ $\dfrac{dy}{dx}=\dfrac{du}{dx}\times \dfrac{dy}{du}$ $\dfrac{dy}{dx}=2x\times 3u^{2}$ $\dfrac{dy}{dx}=6xu^{2}=6x(x^{2}-1)^{2}$
Let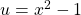 and
and 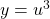
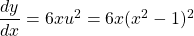
See lessIf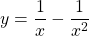 , find
, find 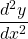
$y=x^{-1}-x^{-2}$ $\dfrac{dy}{dx}=-1\times x^{-1-1}-(-2)\times x^{-2-1}$ $\dfrac{dy}{dx}=-x^{-2}+2x^{-3}$ $\dfrac{dy}{dx}=-\dfrac{1}{x^{2}}+\dfrac{1}{x^{3}}$ $\dfrac{d^{2}y}{dx^{2}}=-2\times -x^{-2-1}+(-3)\times x^{-3-1}$ $\dfrac{d^{2}y}{dx^{2}}=2x^{-3}-3x^{-4}$ $\dfrac{d^{2}y}{dx^{2}}=}=\dfrac{2}{xRead more
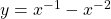
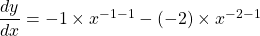
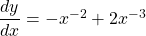
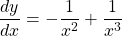
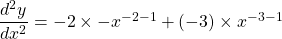
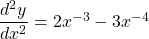
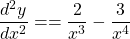
See lessIf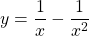 , find
, find 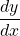
$y=x^{-1}-x^{-2}$ $\dfrac{dy}{dx}=-1\times x^{-1-1}-(-2)\times x^{-2-1}$ $\dfrac{dy}{dx}=-x^{-2}+2x^{-3}$ $\dfrac{dy}{dx}=-\dfrac{1}{x^{2}}+\dfrac{2}{x^{3}}$
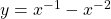
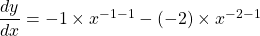
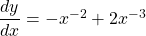
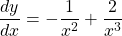
See lessIf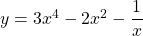 , find
, find 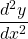
$y=3x^{4}-2x^{2}-x^{-1}$ $\dfrac{dy}{dx}=4\times 3x^{4-1}-2\times 2x^{2-1}-(-1)\times x^{-1-1}$ $\dfrac{dy}{dx}=12x^{3}-4x+x^{-2}$ $\dfrac{dy}{dx}=12x^{3}-4x+\dfrac{1}{x^{2}}$ $\dfrac{d^{2}y}{dx^{2}}=3\times 12x^{3-1}-4x^{1-1}+(-2)\times x^{-2-1}$ $\dfrac{d^{2}y}{dx^{2}}=36x^{2}-4-2x^{-3}$ $\dfrac{dRead more
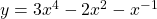
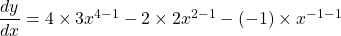
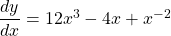
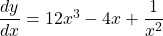
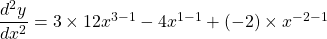
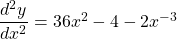
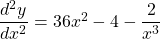
See lessIf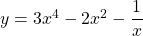 , find
, find 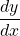
$y=3x^{4}-2x^{2}-x^{-1}$ $\dfrac{dy}{dx}=4\times 3x^{4-1}-2\times 2x^{2-1}-(-1)\times x^{-1-1}$ $\dfrac{dy}{dx}=12x^{3}-4x+x^{-2}$ $\dfrac{dy}{dx}=12x^{3}-4x+\dfrac{1}{x^{2}}$
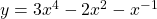
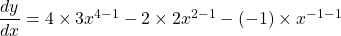
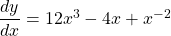
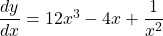
See less