Home> Questions>Q 6334
Next
In Process

AcedStudy Latest Questions

Aldrichyang
  • 0
Tyro
Asked: 2021-04-08T14:28:10+00:00 In: ,

APPLICATION OF DERIVATIVES

  • 0

A supermarket employee wants to construct an open-top box from a 10 inch × 16 inch (in) piece of cardboard.
To do this, the employee plans to cut out squares of equal size from the four corners so that the four sides can
be bent upward. What size should the squares be to create a box with the largest possible volume?

problem solving

You must login to add an answer.

Need An Account,

1 Answer

  2. acedstud

    Here, when the squares are cut and the cardboard folded, the sides of the squares cut out are equivalent to the height of the open-top box formed, hence the changing variable in the volume of the box is the height, h.

    Let the length of the sides of the squares cut out be, h, then the dimensions of the base of the box, after the squares are cut out is (10 – 2h) inch by (16 – 2h) inch.        (because the length of the square cut out is h, and the square is cut out from two sides of each dimension of the cardboard.)

    The volume, V, of a box is given by the product of the area of the base and the height. Thus,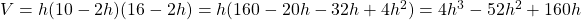 V=h(10-2h)(16-2h)=h(160-20h-32h+4h^2)=4h^3-52h^2+160h

    For the volume to be maximum,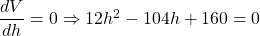 \dfrac{dV}{dh}=0\Rightarrow12h^2-104h+160=0.

    Dividing through by 4, we have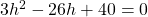 3h^2-26h+40=0.

    Using the quadratic formula, we have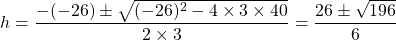 h=\dfrac{-(-26)\pm\sqrt{(-26)^2-4\times3\times40}}{2\times3}=\dfrac{26\pm\sqrt{196}}{6}

    =\dfrac{26+14}{6} or \dfrac{26-14}{6}

    \Rightarrow h=6.667 or h=2

    But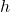 h cannot be 6.667 as we cannot cut out squares of length 6.667 inch from two ends of the 10 inch side of the cardboard as 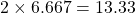2\times6.667=13.33 is greater than 10.

    Thus, the squares to be cut out should be of side lengths 2 inch.

    You can also confirm this using the second derivative test.

Related Questions