G is the event ‘Donna throws two fair dice and gets a total of 3’. H is the event ‘Donna throws two fair dice and gets one odd and one even number’. Are events G and H independent? Justify your answer.
Lost your password? Please enter your email address. You will receive a link and will create a new password via email.
Please briefly explain why you feel this question should be reported.
Please briefly explain why you feel this answer should be reported.
Please briefly explain why you feel this user should be reported.
G is the event ‘Donna throws two fair dice and gets a total of 3’. H is the event ‘Donna throws two fair dice and gets one odd and one even number’. Are events G and H independent? Justify your answer.
For event G (getting a total of 3 with two dice), there are two possible outcomes: (1, 2) and (2, 1). So, the probability of event Q is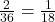
.
For event H (getting one odd and one even number), there are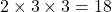
possible outcomes: (1, 2), (1, 4), (1, 6), (3, 2), (3, 4), (3, 6), (5, 2), (5, 4), (5, 6), (2, 1), (2, 3), (2, 5), (4, 1), (4, 3), (4, 5), (6, 1), (6, 3), and (6, 5). So, the probability of event S is 
.
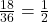Now, consider P(G and H), the probability of both events happening. Two outcomes satisfy both events: (1, 2) and (2, 1). So, P(G and H)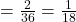
.
Using the formula for independence, P(G and H)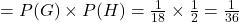
.
Since, the probability of both events happening is not equal to the product of the probabilities of the individual events, we conclude that events G and H are not independent.