what is the area of circle using integration method






Lost your password? Please enter your email address. You will receive a link and will create a new password via email.
Please briefly explain why you feel this question should be reported.
Please briefly explain why you feel this answer should be reported.
Please briefly explain why you feel this user should be reported.
The equation of a circle with radius, r, is given by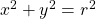 .
.
Making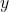 the subject of the formula, we have
the subject of the formula, we have 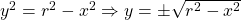 .
.
Now, the radius of a circle divides the circle into four equal parts called the quadrants. And the area of the portion bounded by a curve between two points on the x-axis is given by the integral between the two points of the curve.
Thus, the area of a quadrant of a circle bounded by the center of the circle and the circumference (that is, the radius) is given by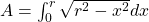 [Note that Area is always positive so we take the positive value of
[Note that Area is always positive so we take the positive value of 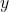 .]
.]
Thus, the area of the 4 quadrants of a circle is given by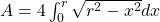 .
.
Converting to polar coordinates,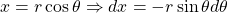 . When
. When 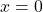 ,
, 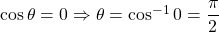 and when
and when  ,
, 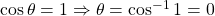
Thus,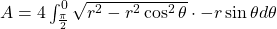
Using the two trigonometric identities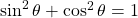 and
and 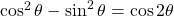 , we have that
, we have that 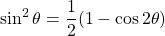 .
.
Thus we have,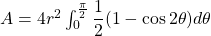
Therefore, the area of a circle with a radius of r is given by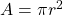 .
.