Find the volume of the solid generated when the indicated plane region is revolved about
the axis of revolution. The region bounded by y = x
2 − 2x + 1, y = 7 − x about y = −1.
nicoletugayTyro






Lost your password? Please enter your email address. You will receive a link and will create a new password via email.
Please briefly explain why you feel this question should be reported.
Please briefly explain why you feel this answer should be reported.
Please briefly explain why you feel this user should be reported.
The sketch of the solid formed by the revolving the region bounded by and
and 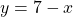 about
about 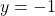 is shown in the attached figure.
is shown in the attached figure.
From the figure, if we slice out tiny pieces of the solid, we will have cylinders with a height of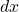 , and the base area of
, and the base area of 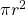 , where
, where  is the radius of the outer shell minus the radius of the inner shell. Notice that the outer shell is made by the line
is the radius of the outer shell minus the radius of the inner shell. Notice that the outer shell is made by the line 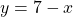 and because the axis of revolution is
and because the axis of revolution is 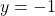 , the radius of the outer shell (distance from the axis of revolution) is given by
, the radius of the outer shell (distance from the axis of revolution) is given by 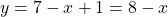 . Similarly, the inner shell is made by the curve
. Similarly, the inner shell is made by the curve  and because the axis of revolution is
and because the axis of revolution is 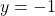 , the radius of the inner shell (distance from the axis of revolution) is given by
, the radius of the inner shell (distance from the axis of revolution) is given by 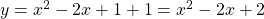 .
.
Thus, the base area of each slice of cylinder is given by![Rendered by QuickLaTeX.com \pi(8-x)^2-\pi(x^2-2x+2)^2=\pi[(64-16x+x^2)-(x^4-4x^3+6x^2-4x+1)]](https://acedstudy.com/wp-content/ql-cache/quicklatex.com-849057fe8f0280297e5ebb3de8fe8646_l3.png) .
.
Thus, the volume of the solid formed by revolving the region bounded by and
and 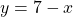 about
about 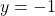 is given by
is given by ![Rendered by QuickLaTeX.com \pi\int_{-2}^3{63-12x-5x^2+4x^3-x^4}dx=\pi\left[63x-6x^2-\dfrac{5}{3}x^3+x^4-\dfrac{1}{5}x^5\right]_{-2}^3](https://acedstudy.com/wp-content/ql-cache/quicklatex.com-b06f5883bf3a25913da522038591b617_l3.png)