Differentiate ![]() wrt x
wrt x






Lost your password? Please enter your email address. You will receive a link and will create a new password via email.
Please briefly explain why you feel this question should be reported.
Please briefly explain why you feel this answer should be reported.
Please briefly explain why you feel this user should be reported.
Let and
and 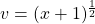
To differentiate the function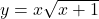 with respect to
with respect to  , you can use the product rule. The product rule states that if you have a function of the form
, you can use the product rule. The product rule states that if you have a function of the form 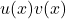 , the derivative is given by:
, the derivative is given by:
In this case, let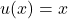 and
and 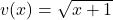 . We need to find their derivatives:
. We need to find their derivatives:
1.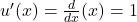 (the derivative of
(the derivative of 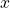 is 1).
is 1).
2. To find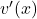 , you can use the chain rule. Let
, you can use the chain rule. Let 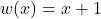 , so
, so 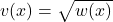 . Now, we can find
. Now, we can find 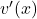 :
:
Now, find![Rendered by QuickLaTeX.com \frac{d}{dx}[w(x)]](https://acedstudy.com/wp-content/ql-cache/quicklatex.com-36d421773cfe565ffe6e0c08aa5fa6a3_l3.png) :
:
Now, we can compute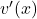 :
:
Now, apply the product rule to find![Rendered by QuickLaTeX.com \frac{d}{dx}[x\sqrt{x+1}]](https://acedstudy.com/wp-content/ql-cache/quicklatex.com-e2de81c4709f14e904c7b48bd92fa210_l3.png) :
:
Now, simplify this expression:
So, the derivative of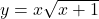 with respect to
with respect to 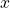 is:
is: