Find ![]() , if
, if ![]()






Lost your password? Please enter your email address. You will receive a link and will create a new password via email.
Please briefly explain why you feel this question should be reported.
Please briefly explain why you feel this answer should be reported.
Please briefly explain why you feel this user should be reported.
To find given
given 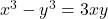 , you can use implicit differentiation. The equation is not given in the form
, you can use implicit differentiation. The equation is not given in the form 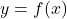 , so we will differentiate both sides of the equation with respect to
, so we will differentiate both sides of the equation with respect to  using implicit differentiation.
using implicit differentiation.
Start by differentiating both sides of the equation:
Now, differentiate each term on the left side of the equation separately:
1.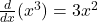 .
.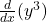 is a bit more involved because it’s a composite function. You can use the chain rule, which states that
is a bit more involved because it’s a composite function. You can use the chain rule, which states that ![Rendered by QuickLaTeX.com \frac{d}{dx}[f(g(x))] = f'(g(x)) \cdot g'(x)](https://acedstudy.com/wp-content/ql-cache/quicklatex.com-ada36a3a6c1a1ca9ebc1d52e8fcce5e1_l3.png) . In this case,
. In this case, 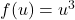 and
and 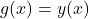 . So, applying the chain rule:
. So, applying the chain rule:
2.
Now, differentiate the right side of the equation:
Now, you can rewrite the equation with these derivatives:
Now, isolate the term with :
:
Factor out :
:
Now, solve for by dividing both sides by
by dividing both sides by 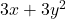 :
:
Simplify the expression:
So,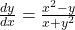 if
if 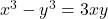 .
.