what is the definition of One-to-One Function and Harizontal Line Test?






Lost your password? Please enter your email address. You will receive a link and will create a new password via email.
Please briefly explain why you feel this question should be reported.
Please briefly explain why you feel this answer should be reported.
Please briefly explain why you feel this user should be reported.
It very well may be characterized as every component of Set A has a remarkable component on Set B.
To sum things up, let us consider ‘f’ is a capacity whose space is set A. The capacity is supposed to be injective if for all x and y in A,
At whatever point f(x)=f(y), at that point x=y
Furthermore, comparably, on the off chance that x ≠ y, f(x) ≠ f(y)
Officially, it is expressed as, assuming f(x) = f(y) infers x=y, f is balanced planned, or f is 1-1.
Essentially, if “f” is a capacity which is coordinated, with space An and range B, at that point the reverse of capacity f is given by;
f-1(y) = x ; if and just if f(x) = y
A capacity f : X → Y is supposed to be coordinated (or injective capacity), if the pictures of particular components of X under f are unmistakable, i.e., for each x1 , x2 ∈ X, f(x1 ) = f(x2 ) infers x1 = x2 . Else, it is called numerous to one capacity.
In Maths, an injective capacity or infusion or one-one capacity is a capacity that involves singularity that never maps discrete components of its space to the same component of its codomain. We can say, each component of the codomain is the picture of just a single component of its area.
A mapping is said to be one-to-one if every element in the range is mapped to exactly one element in the domain.
Consider the mapping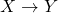 , defined by the relation
, defined by the relation 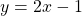 .
.
If X = {1, 2, 8} and Y = {1, 3, 15}, then we say that the mapping is one-to-one as all elements in Y are mapped to exactly one element in X.
A horizontal line test is a test used to find out whether a function has an inverse.