JOEL is a square with diagonals JE and OL intersecting at point M

Question

marcusbautista11Tyro

Asked: March 30, 20212021-03-30T06:03:08+00:00 2021-03-30T06:03:08+00:00In: Middle School/Junior Secondary School

if JM=12, then JE=?

if OL=26 then ML=?

Leave an answer

acedstud · Answer 1 · 2021-03-30T06:24:21+00:00

acedstud

We will look at some properties of a square.

a.) All the sides are equal.

b.) The lengths of the diagonals are equal.

c.) The diagonals bisect each other.

a.) From property (c), JE is a diagonal of square JOEL and JM is half the diagonal JE.

Thus, if JM = 12, then JE =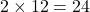 $2\times12=24$ .

b.) OL is a diagonal of square JOEL and ML is half the diagonal OL.

Thus, if OL = 26, then ML is half of 26 =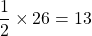 $\dfrac{1}{2}\times26=13$ .

Sasmita · Answer 2 · 2021-03-30T07:01:42+00:00

To calculate the diagonal of a square, multiply the length of the side by the

d = a√2

Where does this equation come from? You can derive this diagonal of square formula e.g. from pythogorous theorm

As we noticed before, the diagonal of a square divides the square into two congruent right triangles.
Legs are square sides and the length of diagonal of the square is the hypotenuse. Given the side length of the square:
a² + a² = diagonal²

diagonal = √(a² + a²) = √(2 * a²) which simplifies to

diagonal = a√2

If you don’t have the side of a square given, use other formulas:

JM=12,

OL=26

area=side*side

side=a=A=338≈18.38478

ME= JE/2

JE=ME*2=12*2=24 (but both diagonal shoud same if it is square)

OL=26

MO=OL/2=26/2=13