The grades of a group of 1000 students in an exam are normally distributed with a mean of 70 and a standard deviation of 10. A student from this group is selected randomly.
a) Find the probability that his/her grade is greater than 80.
b) Find the probability that his/her grade is less than 50.
c) Find the probability that his/her grade is between 50 and 80.
d) Approximately, how many students have grades greater than 80?
RainielFornolesTyro

Let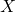 be a random variable representing the grade of a student in the exam, then the probability that
be a random variable representing the grade of a student in the exam, then the probability that 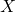 is less than a value,
is less than a value,  , is equivalent to the area under the standard normal curve with
, is equivalent to the area under the standard normal curve with  -score given by
-score given by 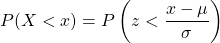 , where
, where 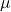 is the mean/average and
is the mean/average and 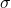 is the standard deviation.
is the standard deviation.
Here,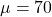 and
and 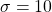 .
.
a.) Thus,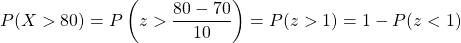 . Using the table of areas under the standard normal curve or a calculator, we have
. Using the table of areas under the standard normal curve or a calculator, we have 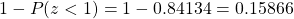 .
.
b.)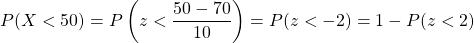 . Using the table of areas under the standard normal curve or a calculator, we have
. Using the table of areas under the standard normal curve or a calculator, we have 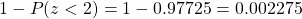 .
.
c.)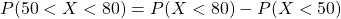
d.) From (a), P(X > 80) = 0.15866. Thus, given that there are 1000 students, the number of students expected to have a grade greater than 80 is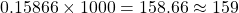 students.
students.