A homework consist of 40 independent problems is given. On the average, it takes 5 minutes to solve a problem, with a standard deviation or 2 minutes. Find the probability that the homework will be completed in less than 3 hours






Lost your password? Please enter your email address. You will receive a link and will create a new password via email.
Please briefly explain why you feel this question should be reported.
Please briefly explain why you feel this answer should be reported.
Please briefly explain why you feel this user should be reported.
Let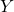 be a random variable representing the amount of time it takes to solve a problem, then
be a random variable representing the amount of time it takes to solve a problem, then 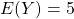 minutes and
minutes and 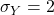 minutes.
minutes.
Let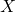 be a random variable representing the amount of time it takes to solve 40 problems, the
be a random variable representing the amount of time it takes to solve 40 problems, the 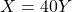 .
.
Using the laws of expected value and variance,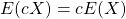 and
and 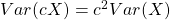 , where
, where  is a constant and
is a constant and 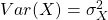 , we have that
, we have that 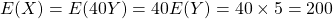 minutes and
minutes and 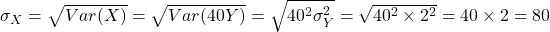 minutes.
minutes.
The probability that a normally distributed variable, X, with a mean,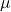 , and standard deviation,
, and standard deviation, 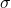 , is less than a value,
, is less than a value,  is given by
is given by 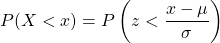 , where
, where  is the area under the standard normal curve.
is the area under the standard normal curve.
Given: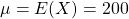 minutes,
minutes, 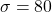 minutes, 3 hours
minutes, 3 hours  180 minutes.
180 minutes.
Thus,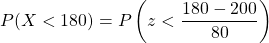
Using the table of the area under the standard normal curve or a calculator, we have that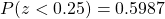 .
.
Therefore, the probability that the home work will be completed in less than 3 hours is 1 – 0.5987 = 0.4013.