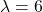Home> Questions>Q 4248
Next
In Process

AcedStudy Latest Questions

acedstud
  • 0
Asked: 2021-03-22T05:42:30+00:00 In: ,

Question of the Day (22/03/2021)

  • 0

The number of accidents that occur on a long stretch of road follows a Poisson distribution with an average of 2 accidents per month.

a.) Find the probability that (i) 4 accidents (ii) at least 1 accident occur on the road next month.

b.) What is the expected number of accidents on the road in the next three months?

c.) What is the probability that 10 accidents occur on the road in the next 3 months?

discrete probabilitypoisson distributionprobabilityprobability distributionstatistics

You must login to add an answer.

Need An Account,

1 Answer

  2. acedstud

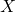    Let X be a random variable representing the number of accidents that occur on the stretch of the road in a certain month, then since 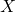X follows a Poisson distribution, 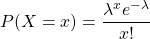P(X=x)=\dfrac{\lambda^xe^{-\lambda}}{x!}, where 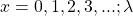x=0,1,2,3,...; \lambda is the average number of accidents on the road per month and e is the exponential constant which is approximately 2.71828.

    a.) Given: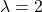 \lambda=2

    (i) P(X=4)=\dfrac{2^4e^{-2}}{4!}=\dfrac{16\times0.135335}{4\times3\times2\times1}=\dfrac{2.16536}{24}=0.0902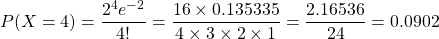

    (ii) The probability of at least 1 accident means the probability of 1 or more accidents. That is,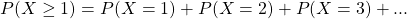 P(X\ge 1)=P(X=1)+P(X=2)+P(X=3)+.... Using the compliment law of probabilities, we have P(X\ge 1)=1-P(X=0).

    P(X=0)=\dfrac{2^0e^{-2}}{0!}=\dfrac{1\times0.135335}{1}=0.135335

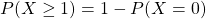    Therefore,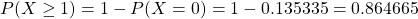 P(X\ge 1)=1-P(X=0)=1-0.135335=0.864665

     

    b.) Since the average number (expected number) of accidents per month is 2, the expected number of accidents in three months is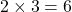 2\times3=6 accidents.

     

    c.) Let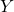 Y be a random variable representing the number of accidents that occur on the stretch of the road in a certain three months. In three months, the average number (expected number) of accidents is 6, so \lambda=6

    P(X=10)=\dfrac{6^{10}e^{-6}}{10!}=0.0413

Related Questions