Solve the center, focus, vertex, latus rectum of the given
(x^2/9)+(y^2/36)=1






Lost your password? Please enter your email address. You will receive a link and will create a new password via email.
Please briefly explain why you feel this question should be reported.
Please briefly explain why you feel this answer should be reported.
Please briefly explain why you feel this user should be reported.
The standard form of the equation of an ellipse centered at (h, k) with the major axis at the y-axis is given by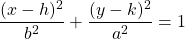 , where
, where 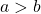 .
.
Comparing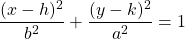 and
and 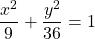 , we can see that h = 0 and k = 0. Therefore, the center of the ellipse is at the origin, (0, 0).
, we can see that h = 0 and k = 0. Therefore, the center of the ellipse is at the origin, (0, 0).
The coordinates of the vertices of an ellipse centered at (0, 0) and with the major axis in the y-axis is given by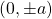 . In this case, the vertices are at points
. In this case, the vertices are at points 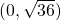 and
and 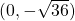 . That is,
. That is, 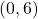 and
and 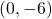 .
.
The equations of the directrices of an ellipse centered at (0, 0) with the major axis in the y-axis is given by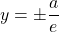 , where
, where  is the eccentricity of the ellipse given by
is the eccentricity of the ellipse given by 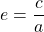 , where
, where  is the length of the foci obtained by
is the length of the foci obtained by 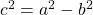 . Here,
. Here, 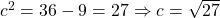 . Thus,
. Thus, 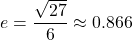 . Therefore, the equations of the directrices are
. Therefore, the equations of the directrices are 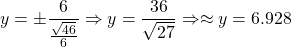 .
.
The length of the latus rectum,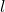 , of an ellipse centered at (0, 0) and with the major axis in the y-axis is given by
, of an ellipse centered at (0, 0) and with the major axis in the y-axis is given by 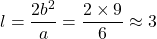 .
.