Solve for the vertex, focus, axis of symmetry, latus rectum and the opening of the parabola
(y+2)^2 = 20(x+3)






Lost your password? Please enter your email address. You will receive a link and will create a new password via email.
Please briefly explain why you feel this question should be reported.
Please briefly explain why you feel this answer should be reported.
Please briefly explain why you feel this user should be reported.
The variable having squared determines the opening of a parabola. If is the squared variable, then the parabola opens up or down but if
is the squared variable, then the parabola opens up or down but if 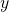 is the squared variable, then the parabola opens left or right. Here, the y variable is squared and the coefficient is positive, therefore, the parabola opens to the right.
is the squared variable, then the parabola opens left or right. Here, the y variable is squared and the coefficient is positive, therefore, the parabola opens to the right.
The vertex form of the equation of a right-opened parabola with vertex (h, k), is given by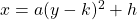 or
or 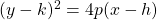 , where
, where 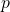 is the distance from the vertex to the focus of the parabola. Given
is the distance from the vertex to the focus of the parabola. Given 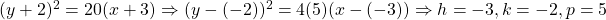 . Therefore, the vertex is at (-3, -2).
. Therefore, the vertex is at (-3, -2).
The focus of a right-opened parabola with vertex (h, k), is given by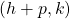 . Thus the focus of the given parabola is at
. Thus the focus of the given parabola is at 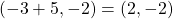 .
.
The axis of symmetry of a right-opened parabola with vertex (h, k), is given by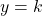 . Thus the axis of symmetry of the given parabola is at
. Thus the axis of symmetry of the given parabola is at 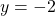 .
.
The length of the latus rectum of a parabola is given by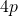 . Thus the length of the latus rectum of the given parabola is at
. Thus the length of the latus rectum of the given parabola is at 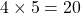 .
.