Center at (4,5) , tangent to x axis






Lost your password? Please enter your email address. You will receive a link and will create a new password via email.
Please briefly explain why you feel this question should be reported.
Please briefly explain why you feel this answer should be reported.
Please briefly explain why you feel this user should be reported.
The equation of a circle with a center at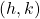 and radius,
and radius,  , is given by
, is given by 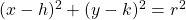 .
.
Here, the center is at (4, 5) so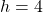 and
and 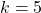 . Since the circle is tangent to the
. Since the circle is tangent to the  -axis, the radius is the length from the center (4, 5) to the
-axis, the radius is the length from the center (4, 5) to the  -axis, which is 5. Thus,
-axis, which is 5. Thus, 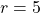 .
.
Therefore, the required equation is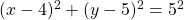 .
.
The equation of a circle is:
(x−h)2+(y−k)2=r2
where (h,k) is the center point and r is the radius
Substitute the center point (4,5) into the standard form:
(x−4)2+(y−5)2=r2
Because the center is 2 units above the x axis and the circle is tangent to the x axis, the radius must be 2:
(x−4)2+(y−5)2=52