Assume that women’s heights are normally distributed with a mean 64.5 in, and a standard deviation of 2.3 in.
a. if 1 woman is randomly selected, find the probability that her height is less than 65 in.
b. if 46 women are randomly selected, find the probability that they have a mean height less than 65 in.

The probability that a normally distributed variable, X, from a sample of size,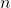 , with a mean,
, with a mean, 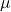 , and standard deviation,
, and standard deviation, 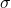 , is less than a value,
, is less than a value,  is given by
is given by 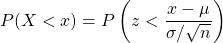 , where
, where  is the area under the standard normal curve.
is the area under the standard normal curve.
Given: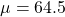 in,
in, 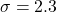 in
in
a.)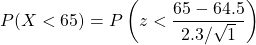
Using the table of the area under the standard normal curve or a calculator, we have that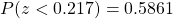 .
.
b.)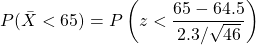
Using the table of the area under the standard normal curve or a calculator, we have that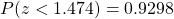 .
.