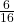A coin is tossed 4 times. Find the probability that exactly 2 heads will appear.






Lost your password? Please enter your email address. You will receive a link and will create a new password via email.
Please briefly explain why you feel this question should be reported.
Please briefly explain why you feel this answer should be reported.
Please briefly explain why you feel this user should be reported.
Let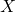 be a random variable representing the number of heads that appear in
be a random variable representing the number of heads that appear in 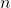 coin tosses, then the probability of success (
coin tosses, then the probability of success (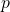 ) is
) is 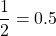 .
.
The probability that a binomial distributed variable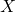 with the number of tries,
with the number of tries, 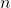 , and the probability of success,
, and the probability of success, 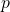 is equal to a value
is equal to a value  is given by
is given by 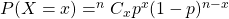 .
.
Here,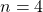 , so the probability that exactly two heads will appear (
, so the probability that exactly two heads will appear (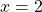 ) is given by
) is given by 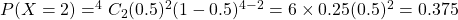
Therefore, the probability that exactly two heads will appear is 0.375.
The 4 stands for 4 tosses while the 2 stands for 2 outcomes(H,T)
Sample space=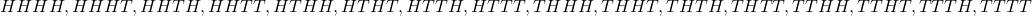
Prob.(exactly two heads) =