Find x,y, and z such that x³+y³+z³=k, for each k from 1 to 100.






Lost your password? Please enter your email address. You will receive a link and will create a new password via email.
Please briefly explain why you feel this question should be reported.
Please briefly explain why you feel this answer should be reported.
Please briefly explain why you feel this user should be reported.
First, we have to restrict x, y, and z to integers otherwise there are infinite combinations satisfying the given equation.
Next, since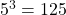 is greater than 100 and
is greater than 100 and 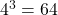 is less than 100, we have that
is less than 100, we have that 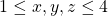 .
.
Thus, the number of possible combinations of (x, y, z) satisfying the given expression is given by the permutation of 4 different objects taking 3 at a time where repetition is allowed given by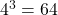 possible combinations.
possible combinations.
Examples, (x, y, z) = (1, 1, 1), (1, 2, 3), (3, 2, 4), etc satisfies the given equation.
However, cases of combinations of more than one 4 or 4 and 3s does not satisfy the equation. That is, (4, 4, 4), (4, 3, 3), (3, 4, 3), (3, 3, 4), (4, 4, 2), (4, 2, 4), (2, 4, 4), (4, 4, 1), (4, 1, 4), (1, 4, 4) does not satisfy the given equation.
Therefore, there are 64 – 10 = 54 possible combinations of values of x, y,, and z satisfying the given equation.