





Lost your password? Please enter your email address. You will receive a link and will create a new password via email.
Please briefly explain why you feel this question should be reported.
Please briefly explain why you feel this answer should be reported.
Please briefly explain why you feel this user should be reported.
Are the events independent?
For event G (getting a total of 3 with two dice), there are two possible outcomes: (1, 2) and (2, 1). So, the probability of event Q is $\frac{2}{36}=\frac{1}{18}$. For event H (getting one odd and one even number), there are $2\times3\times3 = 18$ possible outcomes: (1, 2), (1, 4), (1, 6), (3, 2),Read more
For event G (getting a total of 3 with two dice), there are two possible outcomes: (1, 2) and (2, 1). So, the probability of event Q is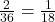 .
.
For event H (getting one odd and one even number), there are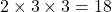 possible outcomes: (1, 2), (1, 4), (1, 6), (3, 2), (3, 4), (3, 6), (5, 2), (5, 4), (5, 6), (2, 1), (2, 3), (2, 5), (4, 1), (4, 3), (4, 5), (6, 1), (6, 3), and (6, 5). So, the probability of event S is
possible outcomes: (1, 2), (1, 4), (1, 6), (3, 2), (3, 4), (3, 6), (5, 2), (5, 4), (5, 6), (2, 1), (2, 3), (2, 5), (4, 1), (4, 3), (4, 5), (6, 1), (6, 3), and (6, 5). So, the probability of event S is 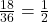 .
.
Now, consider P(G and H), the probability of both events happening. Two outcomes satisfy both events: (1, 2) and (2, 1). So, P(G and H)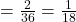 .
.
Using the formula for independence, P(G and H)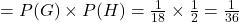 .
.
Since, the probability of both events happening is not equal to the product of the probabilities of the individual events, we conclude that events G and H are not independent.
See lessFind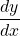 , if
, if 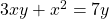
To find $\frac{dy}{dx}$ given $3xy + x^2 = 7y$, you can use implicit differentiation. The equation is not given in the form $y = f(x)$, so we will differentiate both sides of the equation with respect to $x$ using implicit differentiation. Start by differentiating both sides of the equation: $\frac{Read more
To find given
given 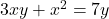 , you can use implicit differentiation. The equation is not given in the form
, you can use implicit differentiation. The equation is not given in the form 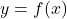 , so we will differentiate both sides of the equation with respect to
, so we will differentiate both sides of the equation with respect to  using implicit differentiation.
using implicit differentiation.
Start by differentiating both sides of the equation:
Now, differentiate each term on the left side of the equation separately:
1.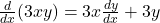 .
.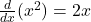 .
.
2.
Now, differentiate the right side of the equation:
Now, you can rewrite the equation with these derivatives:
Now, isolate the term with :
:
Factor out :
:
Now, solve for by dividing both sides by
by dividing both sides by 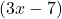 :
:
So,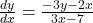 is the derivative with respect to
is the derivative with respect to  of the equation
of the equation 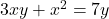 .
.
See lessFind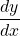 , if
, if 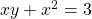
To find $\frac{dy}{dx}$ given $xy + x^2 = 3$, you can use implicit differentiation. The equation is not given in the form $y = f(x)$, so we will differentiate both sides of the equation with respect to $x$ using implicit differentiation. Start by differentiating both sides of the equation: $\frac{d}Read more
To find given
given 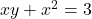 , you can use implicit differentiation. The equation is not given in the form
, you can use implicit differentiation. The equation is not given in the form 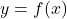 , so we will differentiate both sides of the equation with respect to
, so we will differentiate both sides of the equation with respect to  using implicit differentiation.
using implicit differentiation.
Start by differentiating both sides of the equation:
Now, differentiate each term on the left side of the equation separately:
1.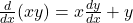 .
.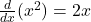 .
.
2.
Now, differentiate the right side of the equation:
Now, you can rewrite the equation with these derivatives:
Now, isolate the term with :
:
Now, solve for by dividing both sides by
by dividing both sides by  :
:
So,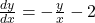 is the derivative with respect to
is the derivative with respect to  of the equation
of the equation 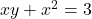 .
.
See lessFind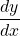 , if
, if 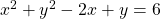
To find $\frac{dy}{dx}$ given $x^2 + y^2 - 2x + y = 6$, you can use implicit differentiation. The equation is not given in the form $y = f(x)$, so we will differentiate both sides of the equation with respect to $x$ using implicit differentiation. Start by differentiating both sides of the equation:Read more
To find given
given 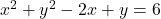 , you can use implicit differentiation. The equation is not given in the form
, you can use implicit differentiation. The equation is not given in the form 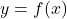 , so we will differentiate both sides of the equation with respect to
, so we will differentiate both sides of the equation with respect to  using implicit differentiation.
using implicit differentiation.
Start by differentiating both sides of the equation:
Now, differentiate each term on the left side of the equation separately:
1.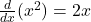 .
.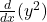 is a bit more involved because it’s a composite function. You can use the chain rule, which states that
is a bit more involved because it’s a composite function. You can use the chain rule, which states that ![Rendered by QuickLaTeX.com \frac{d}{dx}[f(g(x))] = f'(g(x)) \cdot g'(x)](https://acedstudy.com/wp-content/ql-cache/quicklatex.com-ada36a3a6c1a1ca9ebc1d52e8fcce5e1_l3.png) . In this case,
. In this case, 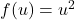 and
and 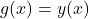 . So, applying the chain rule:
. So, applying the chain rule:
2.
3.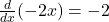 .
.
4.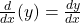 .
.
Now, differentiate the right side of the equation:
Now, you can rewrite the equation with these derivatives:
Now, isolate the term with :
:
Factor out :
:
Now, solve for by dividing both sides by
by dividing both sides by 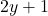 :
:
So,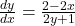 is the derivative with respect to
is the derivative with respect to  of the equation
of the equation 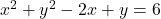 .
.
See lessFind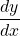 , if
, if 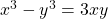
To find $\frac{dy}{dx}$ given $x^3 - y^3 = 3xy$, you can use implicit differentiation. The equation is not given in the form $y = f(x)$, so we will differentiate both sides of the equation with respect to $x$ using implicit differentiation. Start by differentiating both sides of the equation: $\fracRead more
To find given
given 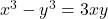 , you can use implicit differentiation. The equation is not given in the form
, you can use implicit differentiation. The equation is not given in the form 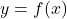 , so we will differentiate both sides of the equation with respect to
, so we will differentiate both sides of the equation with respect to  using implicit differentiation.
using implicit differentiation.
Start by differentiating both sides of the equation:
Now, differentiate each term on the left side of the equation separately:
1.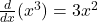 .
.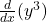 is a bit more involved because it’s a composite function. You can use the chain rule, which states that
is a bit more involved because it’s a composite function. You can use the chain rule, which states that ![Rendered by QuickLaTeX.com \frac{d}{dx}[f(g(x))] = f'(g(x)) \cdot g'(x)](https://acedstudy.com/wp-content/ql-cache/quicklatex.com-ada36a3a6c1a1ca9ebc1d52e8fcce5e1_l3.png) . In this case,
. In this case, 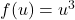 and
and 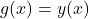 . So, applying the chain rule:
. So, applying the chain rule:
2.
Now, differentiate the right side of the equation:
Now, you can rewrite the equation with these derivatives:
Now, isolate the term with :
:
Factor out :
:
Now, solve for by dividing both sides by
by dividing both sides by 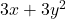 :
:
Simplify the expression:
So,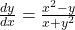 if
if 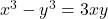 .
.
See lessFind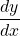 , if
, if 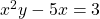
To find $\frac{dy}{dx}$ given $x^2y - 5x = 3$, you can use implicit differentiation. The equation is not given in the form $y = f(x)$, so we will differentiate both sides of the equation with respect to $x$ using implicit differentiation. Start by differentiating both sides of the equation: $$\frac{Read more
To find given
given 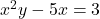 , you can use implicit differentiation. The equation is not given in the form
, you can use implicit differentiation. The equation is not given in the form 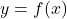 , so we will differentiate both sides of the equation with respect to
, so we will differentiate both sides of the equation with respect to  using implicit differentiation.
using implicit differentiation.
Start by differentiating both sides of the equation:
which can be further simplified as:
(the derivative of a constant, 3, is 0).
Now, apply the product rule to the first term of the equation. Recall that the product rule states:
In our case, let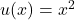 and
and 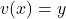 . We also need to differentiate
. We also need to differentiate 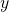 with respect to
with respect to  , which is
, which is  .
.
Now, we can differentiate each term, applying the product rule to the first term:
1.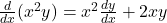 ,
,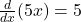 .
.
2.
Now, substitute these results back into the equation:
Now, isolate the term with :
:
Finally, divide by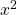 to solve for
to solve for  :
:
So,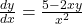 if
if 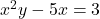 .
.
See lessDifferentiate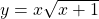 wrt x
wrt x
To differentiate the function $y = x\sqrt{x+1}$ with respect to $x$, you can use the product rule. The product rule states that if you have a function of the form $u(x)v(x)$, the derivative is given by: $\frac{d}{dx}[u(x)v(x)] = u(x)v'(x) + u'(x)v(x)$ In this case, let $u(x) = x$ and $v(x) = \sqrt{xRead more
To differentiate the function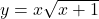 with respect to
with respect to  , you can use the product rule. The product rule states that if you have a function of the form
, you can use the product rule. The product rule states that if you have a function of the form 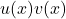 , the derivative is given by:
, the derivative is given by:
In this case, let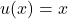 and
and 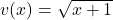 . We need to find their derivatives:
. We need to find their derivatives:
1.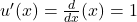 (the derivative of
(the derivative of  is 1).
is 1).
2. To find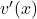 , you can use the chain rule. Let
, you can use the chain rule. Let 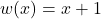 , so
, so 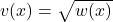 . Now, we can find
. Now, we can find 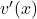 :
:
Now, find![Rendered by QuickLaTeX.com \frac{d}{dx}[w(x)]](https://acedstudy.com/wp-content/ql-cache/quicklatex.com-36d421773cfe565ffe6e0c08aa5fa6a3_l3.png) :
:
Now, we can compute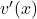 :
:
Now, apply the product rule to find![Rendered by QuickLaTeX.com \frac{d}{dx}[x\sqrt{x+1}]](https://acedstudy.com/wp-content/ql-cache/quicklatex.com-e2de81c4709f14e904c7b48bd92fa210_l3.png) :
:
Now, simplify this expression:
So, the derivative of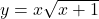 with respect to
with respect to  is:
is:
![Rendered by QuickLaTeX.com \[\frac{d}{dx}[x\sqrt{x+1}] &= \frac{x}{2\sqrt{x+1}} + \sqrt{x+1}\]](https://acedstudy.com/wp-content/ql-cache/quicklatex.com-fd6a048c987144d9f0de91a51ea5bcf4_l3.png)
See lessDifferentiate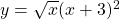 wrt x
wrt x
To differentiate the function $y = \sqrt{x}(x+3)^2$ with respect to $x$, you can use the product rule. The product rule states that if you have a function of the form $u(x)v(x)$, the derivative is given by: $$\frac{d}{dx}[u(x)v(x)] = u(x)v'(x) + u'(x)v(x)$$ In this case, let $u(x) = \sqrt{x}$ and $vRead more
To differentiate the function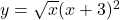 with respect to
with respect to  , you can use the product rule. The product rule states that if you have a function of the form
, you can use the product rule. The product rule states that if you have a function of the form 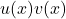 , the derivative is given by:
, the derivative is given by:
In this case, let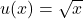 and
and 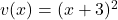 . We need to find their derivatives:
. We need to find their derivatives:
1.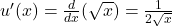 (using the power rule).
(using the power rule).
2.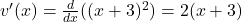 (using the chain rule).
(using the chain rule).
Now, apply the product rule:
Now, simplify this expression:
So, the is the derivative of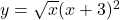 with respect to
with respect to  :
:
![Rendered by QuickLaTeX.com \[2\sqrt{x}(x + 3) + \frac{1}{2\sqrt{x}}(x+3)^2\]](https://acedstudy.com/wp-content/ql-cache/quicklatex.com-8614d2d8dfbb59e4936edea0a954ecd4_l3.png)
See lessWhen working with sets in mathematics, which type of graphical representation can help you understand their relationships?
A Venn diagram is a visual tool used to represent the relationship between sets. It consists of one or more circles that overlap or intersect, with each circle representing a specific set. The overlapping regions show where sets have elements in common, while the non-overlapping parts display elemenRead more
A Venn diagram is a visual tool used to represent the relationship between sets. It consists of one or more circles that overlap or intersect, with each circle representing a specific set. The overlapping regions show where sets have elements in common, while the non-overlapping parts display elements unique to each set. The circles are enclosed inside a rectangle which represents the universal set.
For example, consider the universal set containing positive integers less than 10, and consider two sets: Set A, which contains even numbers, and Set B, which contains multiples of 3.
A Venn diagram for these sets would have one circle representing even numbers and another circle representing multiples of 3. The overlapping section would represent numbers that are both even and multiples of 3, which in this case is 6. The other numbers that are neither even numbers nor multiples of 3 are placed within the rectangle but outside the circles.

See lessTo depict the connections between sets, which graphical representation would you use?
A Venn diagram is a visual tool used to represent the relationship between sets. It consists of one or more circles that overlap or intersect, with each circle representing a specific set. The overlapping regions show where sets have elements in common, while the non-overlapping parts display elemenRead more
A Venn diagram is a visual tool used to represent the relationship between sets. It consists of one or more circles that overlap or intersect, with each circle representing a specific set. The overlapping regions show where sets have elements in common, while the non-overlapping parts display elements unique to each set. The circles are enclosed inside a rectangle which represents the universal set.
For example, consider the universal set containing positive integers less than 10, and consider two sets: Set A, which contains even numbers, and Set B, which contains multiples of 3.
A Venn diagram for these sets would have one circle representing even numbers and another circle representing multiples of 3. The overlapping section would represent numbers that are both even and multiples of 3, which in this case is 6. The other numbers that are neither even numbers nor multiples of 3 are placed within the rectangle but outside the circles.

See less