Home> Questions>Q 4515
Next
In Process
acedstud
Asked: 2021-03-29T07:10:27+00:00 In: ,

Question of the Day (29/03/2021)

Find the derivative of the function y=x^x.

defferentiationderivativederivative of a functionderivative of exponential functionimplicit derivative

Related Questions

2 Answers

  1. To find the derivative of the function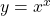 y=x^x, first, we use the logarithm property to evaluate the exponent.

    Thus, taking the logarithm of both sides, we have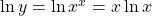 \ln y=\ln{x^x}=x\ln x

    Evaluating the derivative of both sides gives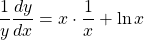 \dfrac{1}{y}\dfrac{dy}{dx}=x\cdot\dfrac{1}{x}+\ln x        [*Note than the right-hand side is a product so we used the product rule of differentiation.]

    Solving algebraically, we have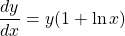 \dfrac{dy}{dx}=y(1+\ln x).

    But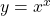 y=x^x, so we have \dfrac{dy}{dx}=x^x(1+\ln x).

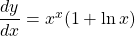    Therefore, the derivative of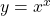 y=x^x is \dfrac{dy}{dx}=x^x(1+\ln x).

    • 0
  2. Tyro
    This answer was edited.

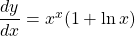    You can use logarithmic differentiation

    Take the natural logarithm of both sides

    ln y=ln xx

    properties of logarithms, rewrite the right hand side

    ln y=x ln x

    Differentiate both sides with respect to x
    Use the  on the right side

    1/y  dy/dx=ln x+x (1/x)

    1/y dy/dx=ln x+1

    Multiply both sides by  y

    dy/dx=y(ln x+1)

    Now y=xx so we can write

    dy/dx=xx(ln x+1)

    • 0
Leave an answer

Leave an answer

Browse