Find ![]() , if
, if ![]()






Lost your password? Please enter your email address. You will receive a link and will create a new password via email.
Please briefly explain why you feel this question should be reported.
Please briefly explain why you feel this answer should be reported.
Please briefly explain why you feel this user should be reported.
To find given
given 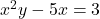 , you can use implicit differentiation. The equation is not given in the form
, you can use implicit differentiation. The equation is not given in the form 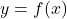 , so we will differentiate both sides of the equation with respect to
, so we will differentiate both sides of the equation with respect to  using implicit differentiation.
using implicit differentiation.
Start by differentiating both sides of the equation:
which can be further simplified as:
(the derivative of a constant, 3, is 0).
Now, apply the product rule to the first term of the equation. Recall that the product rule states:
In our case, let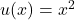 and
and 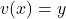 . We also need to differentiate
. We also need to differentiate 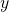 with respect to
with respect to  , which is
, which is  .
.
Now, we can differentiate each term, applying the product rule to the first term:
1.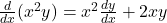 ,
,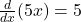 .
.
2.
Now, substitute these results back into the equation:
Now, isolate the term with :
:
Finally, divide by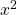 to solve for
to solve for  :
:
So,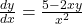 if
if 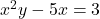 .
.